题目内容
(本小题满分1 4分)已知m,t∈R,函数f (x) =(x - t)3+m.
(I)当t =1时,
(i)若f (1) =1,求函数f (x)的单调区间;
(ii)若关于x的不等式f (x)≥x3—1在区间[1,2]上有解,求m的取值范围;
(Ⅱ)已知曲线y= f (x)在其图象上的两点A(x1,f (x1)),B(x2,f (x2)))( x1≠x2)处的切线
分别为l1、l2.若直线l1与l2平行,试探究点A与点B的关系,并证明你的结论.
【答案】
解:(Ⅰ)(i)因为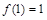 ,所以
,所以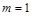 ,·················· 1分
,·················· 1分
则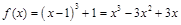 ,
而
,
而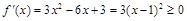 恒成立,
恒成立,
所以函数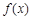 的单调递增区间为
的单调递增区间为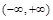 .·············· 4分
.·············· 4分
(ii)不等式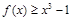 在区间
在区间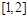 上有解,
上有解,
即 不等式 在区间
在区间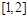 上有解,
上有解,
即 不等式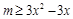 在区间
在区间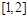 上有解,
上有解,
等价于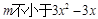 在区间
在区间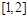 上的最小值,············· 6分
上的最小值,············· 6分
因为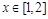 时,
时,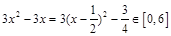 ,
,
所以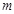 的取值范围是
的取值范围是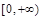 .···················· 9分
.···················· 9分
(Ⅱ)因为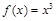 的对称中心为
的对称中心为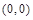 ,
,
而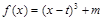 可以由
可以由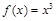 经平移得到,
经平移得到,
所以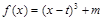 的对称中心为
的对称中心为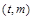 ,故合情猜测,若直线
,故合情猜测,若直线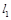 与
与 平行,则点
平行,则点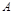 与点
与点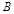 关于点
关于点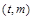 对称. 10分
对称. 10分
对猜想证明如下:
因为
所以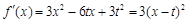
所以,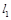 ,
, 的斜率分别为
的斜率分别为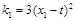 ,
,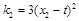 .
.
又直线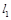 与
与 平行,所以
平行,所以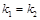 ,即
,即 ,
,
因为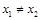 ,
,
所以,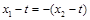 ,························ 12分
,························ 12分
从而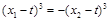 ,
,
所以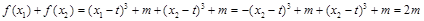 .
.
又由上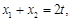
所以点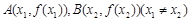 关于点(
关于点(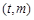 对称.
对称.
故直线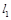 与
与 平行时,点
平行时,点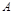 与点
与点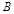 关于点
关于点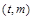 对称.·········· 14分
对称.·········· 14分
【解析】略

练习册系列答案
相关题目

 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD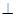 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.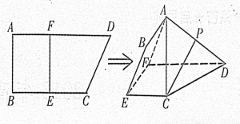
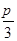 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.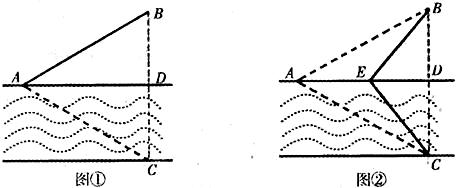
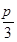 ,AC=4
,AC=4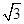 ,D为BC边上一点.
,D为BC边上一点.