题目内容
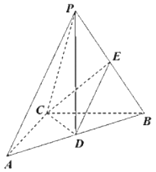
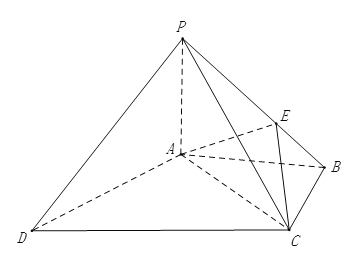
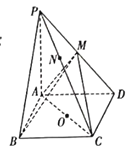
【题目】四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,以
,以![]() 为直径的球面交
为直径的球面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .则点
.则点![]() 到平面
到平面![]() 的距离为_.
的距离为_.
【答案】![]()
【解析】
依题设知,AC是所作球面的直径,则AM⊥MC.由P A⊥平面ABCD,得PA⊥CD,结合CD⊥AD,可得CD⊥平面PAD,则CD⊥AM,再由线面垂直的判定可得A M⊥平面PCD;根据体积相等求出D到平面ACP的距离,即可求得到M与平面APC的距离,再利用等体积求解点![]() 到平面
到平面![]() 的距离即可
的距离即可
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
同理可得![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
由题意可知![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
连接![]() ,
,
又![]() ,所以
,所以![]() 是
是![]() 的中点,
的中点,![]() ,
,
所以![]() ,
,
同理可得![]() ,
,
由题意可知,![]() ,则
,则![]() ,所以
,所以![]()
所以![]()
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,点
,点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,点
,点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由![]() ,得
,得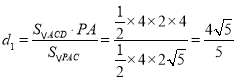
因为![]() 是
是![]() 的中点,所以
的中点,所以![]()
由![]() ,
,
得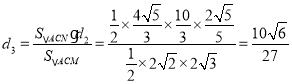
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]()

练习册系列答案
相关题目