题目内容
定义在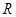 上的函数
上的函数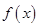 满足
满足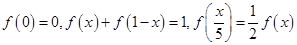 且当
且当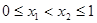 时,
时,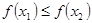 ,则
,则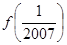 等于
等于
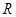 上的函数
上的函数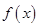 满足
满足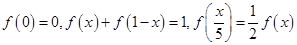 且当
且当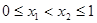 时,
时,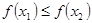 ,则
,则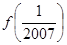 等于
等于A. | B. | C. | D. |
C
:∵f(0)=0,f(x)+f(1-x)=1,令x=1得:f(1)=1,
又f(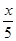 )=
)= f(x),∴当x=1时,f(
f(x),∴当x=1时,f(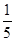 )=
)= f(1)=
f(1)= ;
;
令x=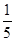 ,由f(
,由f(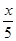 )=
)= f(x)得:
f(x)得:
f(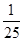 )=
)= f(
f(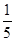 )=
)=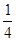 ;同理可求:f(
;同理可求:f(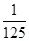 )=
)= f(
f(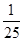 )=
)=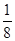 ;
;
f(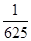 )=)=
)=)= f(
f(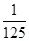 )=
)=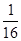 ;
;
f(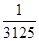 )=
)= f(
f(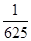 )=
)=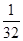 ①
①
再令x= ,由f(x)+f(1-x)=1,可求得f(
,由f(x)+f(1-x)=1,可求得f( )=
)= ,
,
∴f( )+f(1-
)+f(1- )=1,解得f(
)=1,解得f( )=
)= ,
,
令x= ,同理反复利用f(
,同理反复利用f(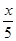 )=
)= f(x),
f(x),
可得f(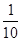 )=)=
)=)= f(
f( )=
)=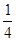 ;
;
f(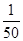 )=
)= f(
f(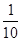 )=
)=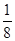 ;…
;…
f(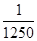 )=
)= f(
f(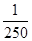 )=
)=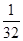 ②
②
由①②可得:,有f(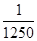 )=f(
)=f(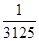 )=
)=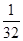 ,
,
∵0≤x1<x2≤1时f(x1)≤f(x2),而0<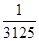 <
<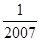 <
<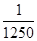 <1
<1
所以有f(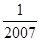 )≥f(
)≥f(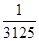 )=
)=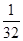 ,
,
f(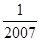 )≤f(
)≤f(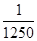 )=
)=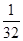 ;
;
故f(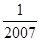 )=
)=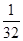 .
.
故选C.
又f(
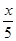 )=
)= f(x),∴当x=1时,f(
f(x),∴当x=1时,f(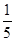 )=
)= f(1)=
f(1)= ;
;令x=
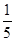 ,由f(
,由f(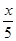 )=
)= f(x)得:
f(x)得:f(
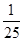 )=
)= f(
f(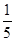 )=
)=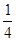 ;同理可求:f(
;同理可求:f(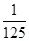 )=
)= f(
f(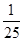 )=
)=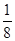 ;
;f(
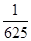 )=)=
)=)= f(
f(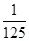 )=
)=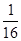 ;
;f(
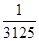 )=
)= f(
f(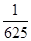 )=
)=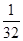 ①
①再令x=
 ,由f(x)+f(1-x)=1,可求得f(
,由f(x)+f(1-x)=1,可求得f( )=
)= ,
,∴f(
 )+f(1-
)+f(1- )=1,解得f(
)=1,解得f( )=
)= ,
,令x=
 ,同理反复利用f(
,同理反复利用f(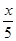 )=
)= f(x),
f(x),可得f(
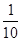 )=)=
)=)= f(
f( )=
)=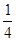 ;
;f(
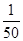 )=
)= f(
f(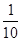 )=
)=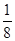 ;…
;…f(
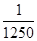 )=
)= f(
f(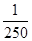 )=
)=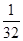 ②
②由①②可得:,有f(
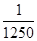 )=f(
)=f(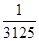 )=
)=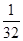 ,
,∵0≤x1<x2≤1时f(x1)≤f(x2),而0<
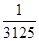 <
<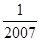 <
<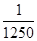 <1
<1所以有f(
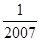 )≥f(
)≥f(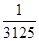 )=
)=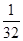 ,
,f(
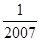 )≤f(
)≤f(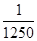 )=
)=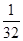 ;
;故f(
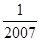 )=
)=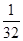 .
.故选C.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
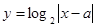 图象的对称轴为
图象的对称轴为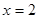 ,则
,则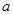 的值为( )
的值为( )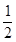
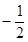
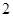
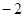
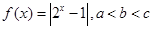 ,且
,且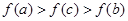 ,则下列结论中,必成立的是( )
,则下列结论中,必成立的是( )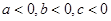

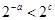
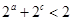
 ,
, 在区间(0,1]上恒成立,试求b的取值范围。
在区间(0,1]上恒成立,试求b的取值范围。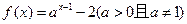 图象恒过定点
图象恒过定点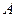 ,且点
,且点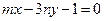 上,则
上,则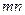 的取值范围为
的取值范围为 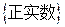 ,
,
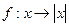 是从A到B的映射;
是从A到B的映射;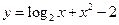 在
在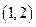 内有一个零点;
内有一个零点;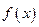 是奇函数,函数
是奇函数,函数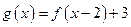 ,则
,则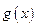 图像的对称中心的坐标
图像的对称中心的坐标 是
是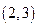 ;
;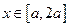 ,都有
,都有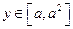 ,且
,且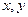 满足方程
满足方程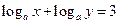 ,这时
,这时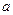 的取值集合为
的取值集合为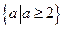 .其中正确的结论序号是
.其中正确的结论序号是  ,
, ,
, ,则
,则 三者的大小关系是( )
三者的大小关系是( )


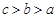
 条件是________。
条件是________。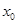 是方程式
是方程式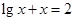 的解,则
的解,则