题目内容

3．已知函数f（x）=axlnx，x∈（0，+∞），其中a为实数，f′（x）为f（x）的导函数，若f′（1）=3，则a的值为3．

分析 由题意求出f'（x），利用f′（1）=3，求a．

解答 解：因为f（x）=axlnx，所以f′（x）=f（x）=lna•axlnx+$\frac{1}{x}$ax，又f′（1）=3，所以a=3；
故答案为：3．

点评 本题考查了求导公式的运用；熟练掌握求导公式是关键．

练习册系列答案
相关题目
13．观察下列等式：
1-$\frac{1}{2}$=$\frac{1}{2}$
1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$=$\frac{1}{3}$+$\frac{1}{4}$
1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{5}$-$\frac{1}{6}$=$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$
…
据此规律，第n个等式可为$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{2n-1}-\frac{1}{2n}$=$\frac{1}{n+1}+\frac{1}{n+2}$+…+$\frac{1}{2n}$．
14．一个二元码是由0和1组成的数字串${x_1}{x_2}…{x_n}（{n∈{N^*}}）$，其中xk（k=1，2，…，n）称为第k位码元，二元码是通信中常用的码，但在通信过程中有时会发生码元错误（即码元由0变为1，或者由1变为0）
已知某种二元码x1x2…x7的码元满足如下校验方程组：$\left\{\begin{array}{l}{x_4}⊕{x_5}⊕{x_6}⊕{x_7}=0\\{x_2}⊕{x_3}⊕{x_6}⊕{x_7}=0\\{x_1}⊕{x_3}⊕{x_5}⊕{x_7}=0\end{array}\right.$
其中运算⊕定义为：0⊕0=0，0⊕1=1，1⊕0=1，1⊕1=0．
现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了1101101，那么利用上述校验方程组可判定k等于5．
11．在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρ（sinθ-3cosθ）=0，曲线C的参数方程为$\left\{\begin{array}{l}{x=t-\frac{1}{t}}\\{y=t+\frac{1}{t}}\end{array}\right.$（ t为参数），l与C相交于A，B两点，则|AB|=$2\sqrt{5}$．
18．阅读如图所示的程序框图，运行相应的程序，则输出i的值为（　　）
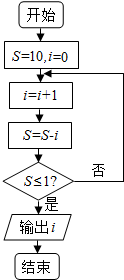
A．2B．3C．4D．5
8．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知△ABC的面积为3$\sqrt{15}$，b-c=2，cosA=-$\frac{1}{4}$．
（Ⅰ）求a和sinC的值；
（Ⅱ）求cos（2A+$\frac{π}{6}$）的值．
15．设α，β是两个不同的平面，l，m是两条不同的直线，且l?α，m?β，（　　）
A．若l⊥β，则α⊥βB．若α⊥β，则l⊥mC．若l∥β，则α∥βD．若α∥β，则l∥m
3．已知点A（1，2）在抛物线C：y2=4x上，过点A作两条直线分别交抛物线于点D，E，直线AD，AE的斜率分别为kAD，KAE．若直线DE过点（-1，-2），则kAD•kAE=（　　）
A．4B．3C．2D．1
3．在△ABC中，A、B、C的对边分别为a、b、c，且bcosC=3acosB-ccosB，$\overrightarrow{BA}$•$\overrightarrow{BC}$=2，则△ABC的面积为（　　）
A．$\sqrt{2}$B．$\frac{3}{2}$C．2$\sqrt{2}$D．4$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网