题目内容
(本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.
,且各局胜负相互独立.
求:(I)打满3局比赛还未停止的概率;
(II)比赛停止时已打局数 的分别列与期望E
的分别列与期望E .
.
 ,且各局胜负相互独立.
,且各局胜负相互独立. 求:(I)打满3局比赛还未停止的概率;
(II)比赛停止时已打局数
 的分别列与期望E
的分别列与期望E .
.(1)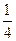 ;(2)略
;(2)略
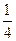 ;(2)略
;(2)略解:令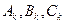 分别表示甲、乙、丙在第k局中获胜.
分别表示甲、乙、丙在第k局中获胜.
(Ⅰ)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满3局比赛还未停止的概率为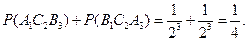 …………………………4分
…………………………4分
(Ⅱ)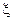 的所有可能值为2,3,4,5,6,且……………………………5分
的所有可能值为2,3,4,5,6,且……………………………5分
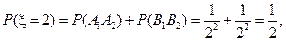
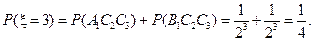
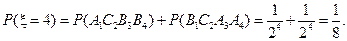
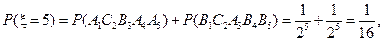
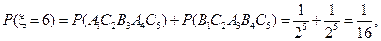 ……9分
……9分
故有分布列
.............10分
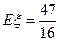
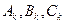 分别表示甲、乙、丙在第k局中获胜.
分别表示甲、乙、丙在第k局中获胜.(Ⅰ)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满3局比赛还未停止的概率为
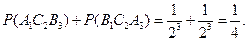 …………………………4分
…………………………4分(Ⅱ)
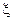 的所有可能值为2,3,4,5,6,且……………………………5分
的所有可能值为2,3,4,5,6,且……………………………5分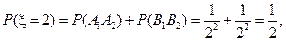
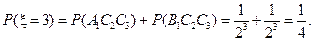
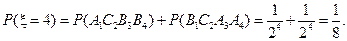
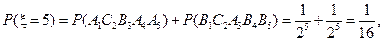
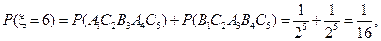 ……9分
……9分故有分布列
 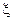 | 2 | 3 | 4 | 5 | 6 |
| P | 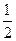 | 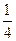 | 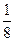 | 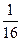 | 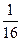 |
.............10分

练习册系列答案
相关题目
 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 ,
,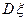 的值.
的值.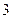 个白球,
个白球, 个红球(所有的球除颜色外其它均相同),从中任取
个红球(所有的球除颜色外其它均相同),从中任取 分,每取一个白球得
分,每取一个白球得 分,每取一个红球得
分,每取一个红球得 ,用随机变量X表示取
,用随机变量X表示取 。已知比赛中,第一局日本女排先胜一局,在这个条件下,(Ⅰ)求中国女排取胜的概率
。已知比赛中,第一局日本女排先胜一局,在这个条件下,(Ⅰ)求中国女排取胜的概率 ,求
,求 ((Ⅰ)(Ⅱ)均用分数作答)
((Ⅰ)(Ⅱ)均用分数作答) ,且P(A)=m,设随机变量x=
,且P(A)=m,设随机变量x= 则x的方差D(x)是:( )
则x的方差D(x)是:( ) 和
和 ,且
,且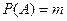 ,令随机变量
,令随机变量 ,则
,则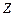 的方差
的方差 等于( )
等于( )

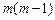

 只小球,用随机变量
只小球,用随机变量 表示摸出的
表示摸出的
 .
.