Question

【题目】已知椭圆C： =1（a＞b＞0）的离心率为 ，且过定点M（1， ）．
（1）求椭圆C的方程；
（2）已知直线l：y=kx﹣ （k∈R）与椭圆C交于A、B两点，试问在y轴上是否存在定点P，使得以弦AB为直径的圆恒过P点？若存在，求出P点的坐标和△PAB的面积的最大值，若不存在，说明理由．

Answer 1

【答案】
（1）解：由已知可得 ，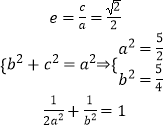

∴椭圆C的方程为

（2）解：由 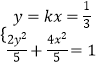得：9（2k2+4）x2﹣12kx﹣43=0①

设A（x1，y1），B（x2，y2），则x1、x2是方程①的两根，

∴ ，

设P（0，p），则 ，

=

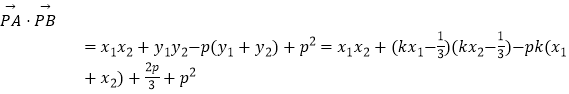
假设在y轴上存在定点P，使得以弦AB为直径的圆恒过P点，

则 ，即 ．

即（18p2﹣45）k2+36p2+24p﹣39=0对任意k∈R恒成立，

∴ ，

此方程组无解，

∴不存在定点满足条件

【解析】（1）运用离心率公式和点M满足椭圆方程，解方程可得a，b，进而得到椭圆方程；（2）联立直线方程和椭圆方程，运用韦达定理，设P（0，p），求得向量PA，PB和数量积，再由直径所对的圆周角为直角，结合向量垂直的条件，即可得到结论．