题目内容
8.某校高二年级开设三门数学选修课程.如果甲、乙两名同学各从中任选一门,那么他们所选课程恰好相同的概率为( )| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
分析 先求出甲乙选课一共有多少种情形,再求出甲乙选择的课程恰好相同,一共有多少种情形,由此利用等可能事件概率计算公式能求出他们所选课程恰好相同的概率.
解答 解:∵某校高二年级开设三门数学选修课程,甲、乙两名同学各从中任选一门,
∴甲乙选课共有3×3=9种情形
甲乙选择的课程恰好相同,共有3种情形,
∴他们所选课程恰好相同的概率P=$\frac{3}{9}$=$\frac{1}{3}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
3.已知集合A={1,2,3},B={2,3,4},那么集合A∩B=( )
| A. | {2} | B. | {2,3} | C. | {1,2,3} | D. | {1,2,3,4} |
 中,侧面
中,侧面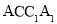 与侧面
与侧面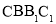 都是菱形,
都是菱形, ,
, .
.
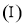 求证:
求证: ;
; 若
若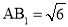 ,求二面角
,求二面角 的余弦值.
的余弦值. 和
和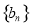 的前
的前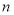 项和分别为
项和分别为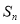 和
和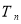 ,已知
,已知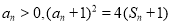 ,
,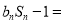
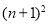 ,其中
,其中 。
。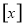 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如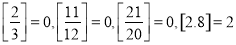 。当
。当 .
.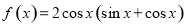 的最大值和最小正周期分别是 ( )
的最大值和最小正周期分别是 ( ) C. 2,2π D.
C. 2,2π D.