题目内容
17.已知函数f(x)=$\frac{1}{3}$x3-ax2+(a2-1)x+b(a,b∈R)(Ⅰ)若x=1为f(x)的极值点,求实数a的值;
(Ⅱ)若y=f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0,求f(x)在区间[-1,4]上的最大值.
分析 (Ⅰ)求出导数,由题意可得f′(1)=0,解方程可得a;
(Ⅱ)求出导数,求得切线的斜率和切点,解方程可得a,b,再由极值和区间[-1,4]的端点处的函数值,即可得到所求最大值.
解答 解:(Ⅰ)由已知得f′(x)=x2-2ax+a2-1,
∵x=1是f(x)的极值点,
∴f′(1)=0,即a2-2a=0.
解a=0,或2.
经检验合题意.故a=0或a=2;
(Ⅱ)∵(1,f(1))是切点,
∴由切线方程x+y-3=0可得1+f(1)-3=0,即f(1)=2,
即$2=\frac{1}{3}-a+{a^2}-1+b,{a^2}-a+b-\frac{8}{3}=0$.
∵切线x+y-3=0的斜率为-1,
∴f′(1)=-1,即a2-2a+1=0,即a=1.
代入解得$b=\frac{8}{3}$.
∴$f(x)=\frac{1}{3}{x^3}-{x^2}+\frac{8}{3}$.
∴f′(x)=x2-2x,∴x=0和x=2是y=f(x)的两个极值点.
∵$f(0)=\frac{8}{3},f(2)=\frac{4}{3},f(-1)=\frac{4}{3},f(4)=8$,
∴y=f(x)在[-1,4]上的最大值为8.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
8.某校高二年级开设三门数学选修课程.如果甲、乙两名同学各从中任选一门,那么他们所选课程恰好相同的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
2.已知集合P={x|-4≤x≤4},Q={y|-2≤y≤2},则下列对应不能表示为从P到Q的函数的是( )
| A. | y=$\frac{1}{2}$x | B. | y2=$\frac{1}{2}$(x+4) | C. | y=$\frac{1}{4}$x2-2 | D. | y=-$\frac{1}{8}$x2 |
 则有 ( )
则有 ( )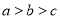 B.
B. 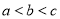 C.
C. 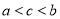 D.
D. 