题目内容
11.若$\underset{lim}{n→∞}$(2n+$\frac{a{n}^{2}-2n-1}{bn+3}$)=$\frac{1}{2}$,则a+b=-8.分析 将原式化为$\underset{lim}{n→∞}$$\frac{(a+2b)n+4-\frac{1}{n}}{b+\frac{3}{n}}$,再取极限.
解答 解:$\underset{lim}{n→∞}$(2n+$\frac{a{n}^{2}-2n-1}{bn+3}$)
=$\underset{lim}{n→∞}$$\frac{2n(bn+3)+an^2-2n-1}{bn+3}$
=$\underset{lim}{n→∞}$$\frac{(a+2b)n^2+4n-1}{bn+3}$
=$\underset{lim}{n→∞}$$\frac{(a+2b)n+4-\frac{1}{n}}{b+\frac{3}{n}}$=$\frac{1}{2}$,
其中,$\underset{lim}{n→∞}$$\frac{1}{n}$=0,要使上式成立,须满足$\left\{\begin{array}{l}{a+2b=0}\\{\frac{4}{b}=\frac{1}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-16}\\{b=8}\end{array}\right.$,所以,a+b=-8,
故答案为:-8.
点评 本题主要考查了极限及其运算,并应用常用极限$\underset{lim}{n→∞}$$\frac{1}{n}$=0解题,属于中档题.

练习册系列答案
相关题目
19.$\frac{\sqrt{3}}{cos10°}$-$\frac{1}{sin170°}$=( )
| A. | -2 | B. | 2 | C. | 4 | D. | -4 |
6.等差数列{an}的前n项和为Sn,若当首项a1和公差d变化时,a3+a10+a11是一个定值,则下列选项中为定值的是( )
| A. | S17 | B. | S16 | C. | S15 | D. | S14 |
16.如图,四面体ABCD中,各棱相等,M是CD的中点,则直线BM与平面ABC所成角的正弦值为( )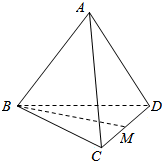

| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
3.函数f(x)=log2(4-x2)定义域为( )
| A. | [-2,2] | B. | (-2,2) | C. | (-∞,2)∪(2,+∞) | D. | (-∞,2]∪[2,+∞) |
20.下列函数中,在区间(0,1)上是增函数的是( )
| A. | y=3-x | B. | y=x | C. | y=$\frac{1}{x}$ | D. | y=-x2 |