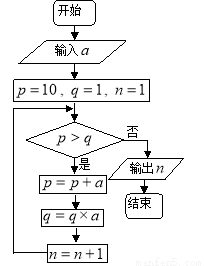
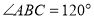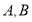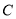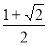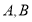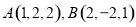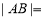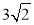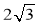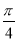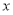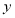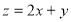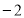题目内容
在圆锥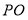 中,已知
中,已知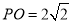 ,
,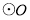 的直径
的直径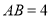 ,点
,点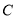 在底面圆周上,且
在底面圆周上,且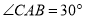 ,
,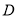 为
为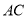 的中点.
的中点.
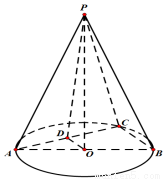
(1)证明: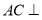 平面
平面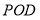 ;
;
(2)求点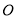 到面
到面 的距离.
的距离.
(1)证明详见解析;(2) .
.
【解析】
试题分析:(1)先证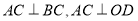 ,再由线面垂直的判定定理证明
,再由线面垂直的判定定理证明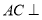 平面
平面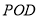 ;(2)作
;(2)作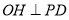 ,垂足为
,垂足为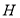 ,可证
,可证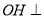 平面
平面 ,在
,在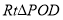 中,利用等面积法可求
中,利用等面积法可求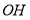 .
.
试题解析:(1)证明: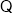
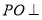 面
面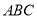 ,且
,且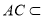 面
面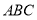

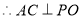 2分
2分
由于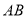 是直径,且点
是直径,且点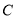 在圆周上,故有
在圆周上,故有
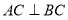
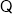 点
点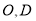 分别是
分别是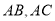 的中点
的中点
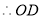 ∥
∥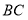
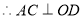 5分
5分
又
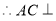 面
面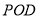 7分
7分
(2)由(1)知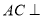 面
面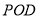 ,又有
,又有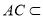 面
面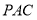
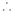 面
面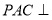 面
面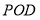 9分
9分
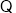 面
面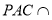 面
面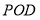 =
=
作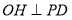 ,垂足为
,垂足为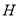 ,则有
,则有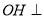 面
面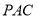
从而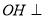 面
面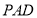 11分
11分
在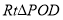 中,
中,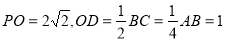
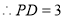 13分
13分
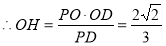 14分
14分
考点:1.空间中的垂直关系;2.空间中的距离问题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目