题目内容
命题“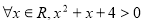 ”的否定是 .
”的否定是 .
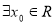 ,
,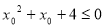
【解析】
试题分析:根据全称命题的否定为特称命题可知,命题“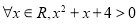 ”的否定为“
”的否定为“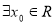 ,
,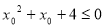 ”.
”.
考点:全称命题与特称命题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
命题“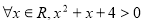 ”的否定是 .
”的否定是 .
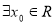 ,
,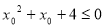
【解析】
试题分析:根据全称命题的否定为特称命题可知,命题“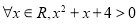 ”的否定为“
”的否定为“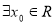 ,
,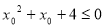 ”.
”.
考点:全称命题与特称命题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案