题目内容
已知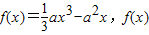 的定义域为R,函数
的定义域为R,函数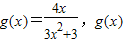 的定义域为[0,2].
的定义域为[0,2].(1)设a≠0,求f(x)的单调区间;
(2)求g(x)的值域;
(3)设a>0,若对任意x1∈[0,2],总存在x∈[0,2],使g(x1)-f(x)=0,求实数a的取值范围.
【答案】分析:(1)先求出其导函数,再根据导函数值的正负来求单调区间即可;
(2)先求出x=0时,g(x)=0;再结合基本不得呢公式求出其他部分的值域,最后综合即可.
(3)先把问题转化为[0, ]⊆A,即转化为求函数f(x)的值域,求出其导函数,结合其单调区间求出最值,即可得到结论.
]⊆A,即转化为求函数f(x)的值域,求出其导函数,结合其单调区间求出最值,即可得到结论.
解答:解:(1)∵f'(x)=ax2-a2,
当a>0时,增区间为(-∞,-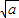 )和(
)和( ,+∞),减区间为(-
,+∞),减区间为(-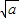 ,
,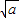 );
);
当a<0时,f'(x)<0恒成立,f(x)在实数集上单调递减.
(2)g(x)=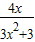 ,x∈[0,2],x=0时,g(x)=0.
,x∈[0,2],x=0时,g(x)=0.
0<x≤2时,g(x)= •
•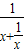 ≤
≤ •
•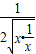 =
= •
• =
= ,且g(x)>0,
,且g(x)>0,
当且仅当x=1时上式取等号,即0<g(x)≤ .
.
综上,g(x)的值域为[0, ].
].
(3)设函数f(x)在[0,2]上的值域是A,
若对任意x1∈[0,2],总存在x∈[0,2]使g(x1)-f(x)=0,
∴[0, ]⊆A
]⊆A
当a>0由f'(x)=ax2-a2=a(x-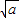 )(x+
)(x+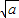 )
)
令f'(x)=0得x=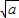 或x=-
或x=-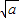 (舍去).
(舍去).
0<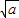 <2时,x,f'(x),f(x)的变化如表,
<2时,x,f'(x),f(x)的变化如表,
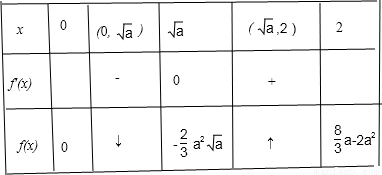
∴f(0)=0,f(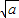 )<0,
)<0,
∴f(2)= a-2a2≥
a-2a2≥ 解得
解得 ≤a≤1.
≤a≤1.
当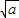 ≥2时,f'(x)<0,
≥2时,f'(x)<0,
∴函数f(x)在(0,2)上单调递减.
∴f(0)=0,f(2)= a-2a2<0,
a-2a2<0,
∴当x∈[0,2]时,不满足[0, ]⊆A.
]⊆A.
综上可知,实数a的取值范围是[ ,1].
,1].
点评:本题主要考查基本不等式的应用以及利用导函数求函数的最值以及单调区间.在利用基本不等式解题时,一定要注意基本不等式使用的条件:一正,二定,三相等.
(2)先求出x=0时,g(x)=0;再结合基本不得呢公式求出其他部分的值域,最后综合即可.
(3)先把问题转化为[0,
 ]⊆A,即转化为求函数f(x)的值域,求出其导函数,结合其单调区间求出最值,即可得到结论.
]⊆A,即转化为求函数f(x)的值域,求出其导函数,结合其单调区间求出最值,即可得到结论.解答:解:(1)∵f'(x)=ax2-a2,
当a>0时,增区间为(-∞,-
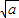 )和(
)和( ,+∞),减区间为(-
,+∞),减区间为(-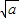 ,
,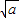 );
);当a<0时,f'(x)<0恒成立,f(x)在实数集上单调递减.
(2)g(x)=
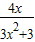 ,x∈[0,2],x=0时,g(x)=0.
,x∈[0,2],x=0时,g(x)=0.0<x≤2时,g(x)=
 •
•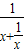 ≤
≤ •
•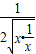 =
= •
• =
= ,且g(x)>0,
,且g(x)>0,当且仅当x=1时上式取等号,即0<g(x)≤
 .
.综上,g(x)的值域为[0,
 ].
].(3)设函数f(x)在[0,2]上的值域是A,
若对任意x1∈[0,2],总存在x∈[0,2]使g(x1)-f(x)=0,
∴[0,
 ]⊆A
]⊆A当a>0由f'(x)=ax2-a2=a(x-
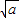 )(x+
)(x+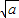 )
)令f'(x)=0得x=
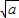 或x=-
或x=-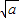 (舍去).
(舍去).0<
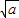 <2时,x,f'(x),f(x)的变化如表,
<2时,x,f'(x),f(x)的变化如表,
∴f(0)=0,f(
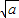 )<0,
)<0,∴f(2)=
 a-2a2≥
a-2a2≥ 解得
解得 ≤a≤1.
≤a≤1.当
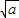 ≥2时,f'(x)<0,
≥2时,f'(x)<0,∴函数f(x)在(0,2)上单调递减.
∴f(0)=0,f(2)=
 a-2a2<0,
a-2a2<0,∴当x∈[0,2]时,不满足[0,
 ]⊆A.
]⊆A.综上可知,实数a的取值范围是[
 ,1].
,1].点评:本题主要考查基本不等式的应用以及利用导函数求函数的最值以及单调区间.在利用基本不等式解题时,一定要注意基本不等式使用的条件:一正,二定,三相等.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知下表为定义域为R的函数f(x)=ax3+cx+d若干自变量取值及其对应函数值,为便于研究,相关函数值非整数值时,取值精确到0.01.
根据表中数据解答下列问题:
(1)函数y=f(x)在区间[0.55,0.6]上是否存在零点,写出判断并说明理由;
(2)证明:函数y=f(x)在区间(-∞,-0.35]单调递减.
| x | 3.27 | 1.57 | -0.61 | -0.59 | 0.26 | 0.42 | -0.35 | -0.56 | 4.25 | |
| y | -101.63 | -10.04 | 0.07 | 0.03 | 0.21 | 0.20 | -0.22 | -0.03 | -226.05 |
(1)函数y=f(x)在区间[0.55,0.6]上是否存在零点,写出判断并说明理由;
(2)证明:函数y=f(x)在区间(-∞,-0.35]单调递减.