题目内容
已知直线 交抛物线
交抛物线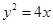 于
于 两点.若该抛物线上存在点
两点.若该抛物线上存在点 ,使得
,使得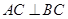 ,则
,则 的取值范围为_________.
的取值范围为_________.
解析试题分析:由题意知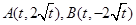 ,设
,设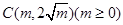 ,由
,由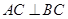 得
得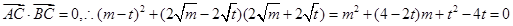 ,
,
解得: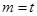 (舍) 或
(舍) 或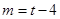 ,由
,由 得
得 的取值范围为
的取值范围为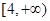 .
.
考点:直线与抛物线的位置关系.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
题目内容
已知直线 交抛物线
交抛物线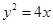 于
于 两点.若该抛物线上存在点
两点.若该抛物线上存在点 ,使得
,使得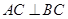 ,则
,则 的取值范围为_________.
的取值范围为_________.
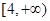
解析试题分析:由题意知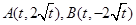 ,设
,设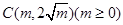 ,由
,由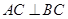 得
得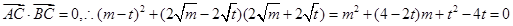 ,
,
解得: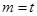 (舍) 或
(舍) 或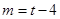 ,由
,由 得
得 的取值范围为
的取值范围为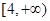 .
.
考点:直线与抛物线的位置关系.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案