题目内容
若不论k为何值,直线 与曲线
与曲线 总有公共点,则
总有公共点,则 的取值范围是( )
的取值范围是( )
A. B.
B.
C. D.
D.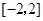
【答案】
B
【解析】
试题分析:把y=k(x-2)+b代入x2-y2=1得x2-[k(x-2)+b]2=1,
△=4k2(b-2k)2+4(1-k2)[(b-2k)2+1]
=4(1-k2)+4(b-2k)2
=4[3k2-4bk+b2+1]=4[3(k2-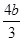 k+
k+ 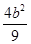 )-
)-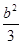 +1]
+1]
不论k取何值,△≥0,则1-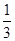 b2≥0
b2≥0
∴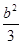 ≤1,∴b2≤3,则-
≤1,∴b2≤3,则-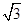 ≤b≤
≤b≤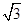 ,故选B。
,故选B。
考点:本题主要考查直线与椭圆的位置关系。
点评:常见题型,联立方程组,整理得一元二次方程,运用根的判别式求参数的范围,是常规解法.

练习册系列答案
相关题目