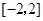题目内容
若不论k为何值,直线y=k(x-2)+b与曲线x2-y2=1总有公共点,则b的取值范围是 .
【答案】分析:把y=k(x-2)+b代入x2-y2=1得(1-k2)x2-2k(b-2k)x-(b-2k)2-1=0,△=4k2(b-2k)2+4(1-k2)[(b-2k)2+1]=4[3(k-2b× 3)2+b2+1-4b2×
3)2+b2+1-4b2× ],不论k取何值,△≥0,所以
],不论k取何值,△≥0,所以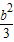 ≤1,由此能求出b的取值范围.
≤1,由此能求出b的取值范围.
解答:解:把y=k(x-2)+b代入x2-y2=1得:
x2-[k(x-2)+b]2=1,
(1-k2)x2-2k(b-2k)x-(b-2k)2-1=0,
△=4k2(b-2k)2+4(1-k2)[(b-2k)2+1]
=4(1-k2)+4(b-2k)2
=4[3k2-4bk+b2+1]
=4[3(k-2b× 3)2+b2+1-4b2×
3)2+b2+1-4b2× ],
],
不论k取何值,△≥0
b2+1-4b2× ≥0
≥0
∴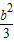 ≤1,
≤1,
b2≤3,
-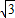 ≤b≤
≤b≤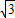 .
.
故答案为:[-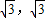 ].
].
点评:本题考查直线与双曲线的性质和应用,解题时要认真审题,仔细解答,注意根的判别式的合理运用.
 3)2+b2+1-4b2×
3)2+b2+1-4b2× ],不论k取何值,△≥0,所以
],不论k取何值,△≥0,所以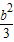 ≤1,由此能求出b的取值范围.
≤1,由此能求出b的取值范围.解答:解:把y=k(x-2)+b代入x2-y2=1得:
x2-[k(x-2)+b]2=1,
(1-k2)x2-2k(b-2k)x-(b-2k)2-1=0,
△=4k2(b-2k)2+4(1-k2)[(b-2k)2+1]
=4(1-k2)+4(b-2k)2
=4[3k2-4bk+b2+1]
=4[3(k-2b×
 3)2+b2+1-4b2×
3)2+b2+1-4b2× ],
],不论k取何值,△≥0
b2+1-4b2×
 ≥0
≥0∴
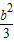 ≤1,
≤1,b2≤3,
-
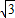 ≤b≤
≤b≤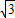 .
.故答案为:[-
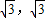 ].
].点评:本题考查直线与双曲线的性质和应用,解题时要认真审题,仔细解答,注意根的判别式的合理运用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 与曲线
与曲线 总有公共点,则
总有公共点,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.