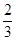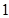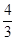题目内容
若A为不等式组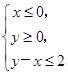 表示的平面区域,则当实数a从-2连续变化到0时,动直线x+y=a扫过A中部分的区域的面积为( )
表示的平面区域,则当实数a从-2连续变化到0时,动直线x+y=a扫过A中部分的区域的面积为( )
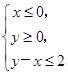 表示的平面区域,则当实数a从-2连续变化到0时,动直线x+y=a扫过A中部分的区域的面积为( )
表示的平面区域,则当实数a从-2连续变化到0时,动直线x+y=a扫过A中部分的区域的面积为( )A.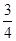 | B.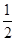 | C.2 | D.1 |
D
A区域为(-2,0),(0,0),(0,2)形成的直角三角形,其面积为2,则直线x+y=a从(-2,0)开始扫过,扫到区域一半时停止,所以扫过A中部分的区域的面积为1.

练习册系列答案
相关题目
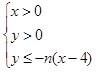 所表示的平面区域为
所表示的平面区域为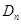 ,记
,记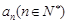 . 则
. 则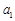 = ,经推理可得到
= ,经推理可得到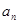 = .
= . , 则目标函数
, 则目标函数 的最大值是 .
的最大值是 .
 则z=2x+y的最小值为( )
则z=2x+y的最小值为( )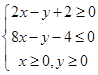 ,若目标函数
,若目标函数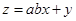 (
(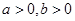 )的最大值为8,则
)的最大值为8,则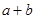 的最小值为 .
的最小值为 . 满足约束条件
满足约束条件 若目标函数
若目标函数 的最大值为
的最大值为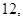 则
则 的最小值为______________ .
的最小值为______________ .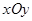 中,已知集合
中,已知集合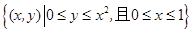 所表示的图形的面积为
所表示的图形的面积为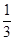 ,若集合
,若集合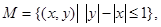
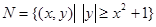 ,则
,则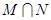 所表示的图形面积为 ( )
所表示的图形面积为 ( )