题目内容
设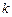 ,
,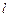 是给定的两个正整数.证明:有无穷多个正整数
是给定的两个正整数.证明:有无穷多个正整数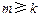 ,使得
,使得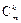 与
与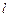 互素.
互素.
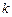 ,
,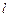 是给定的两个正整数.证明:有无穷多个正整数
是给定的两个正整数.证明:有无穷多个正整数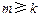 ,使得
,使得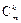 与
与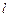 互素.
互素.证法一:对任意正整数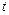 ,令
,令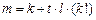 .我们证明
.我们证明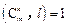 .
.
设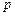 是
是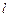 的任一素因子,只要证明:
的任一素因子,只要证明: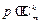 .
.
若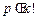 ,则由
,则由
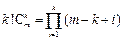
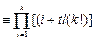
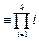
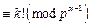 .
.
及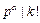 ,且
,且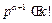 ,知
,知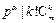 且
且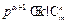 .从而
.从而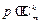 .
.
证法二:对任意正整数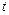 ,令
,令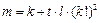 ,我们证明
,我们证明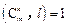 .
.
设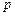 是
是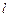 的任一素因子,只要证明:
的任一素因子,只要证明: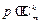 .
.
若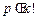 ,则由
,则由
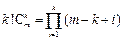
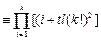
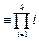
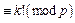 .
.
即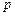 不整除上式,故
不整除上式,故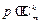 .
.
若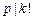 ,设
,设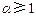 使
使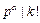 ,但
,但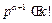 .
.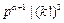 .故由
.故由
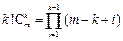
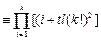
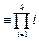
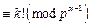
及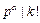 ,且
,且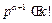 ,知
,知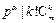 且
且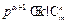 .从而
.从而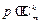 .
.
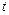 ,令
,令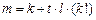 .我们证明
.我们证明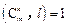 .
.设
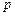 是
是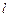 的任一素因子,只要证明:
的任一素因子,只要证明: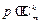 .
.若
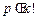 ,则由
,则由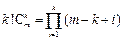
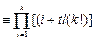
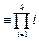
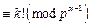 .
.及
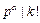 ,且
,且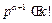 ,知
,知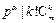 且
且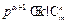 .从而
.从而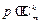 .
.证法二:对任意正整数
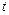 ,令
,令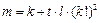 ,我们证明
,我们证明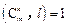 .
.设
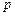 是
是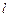 的任一素因子,只要证明:
的任一素因子,只要证明: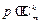 .
.若
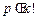 ,则由
,则由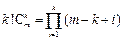
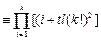
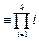
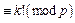 .
.即
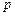 不整除上式,故
不整除上式,故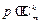 .
.若
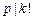 ,设
,设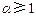 使
使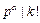 ,但
,但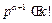 .
.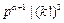 .故由
.故由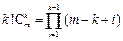
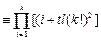
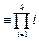
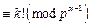
及
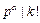 ,且
,且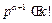 ,知
,知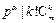 且
且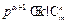 .从而
.从而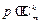 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
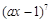 展开式中含
展开式中含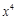 项的系数为
项的系数为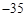 ,则a等于( )
,则a等于( )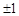

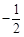
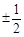
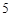 位男生,
位男生,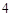 位女生中选派
位女生中选派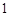 位女生的选法共有
位女生的选法共有 种
种 种
种 种
种 种
种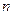 作竖式加法
作竖式加法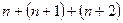 均不产生进位现象,则称
均不产生进位现象,则称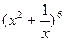 的展开式中,常数项是 。(结果用数值表示)
的展开式中,常数项是 。(结果用数值表示)