题目内容
(本题满分15分)
已知函数f (x)=x 2+ax ,且对任意的实数x都有f (1+x)=f (1-x) 成立.
(1)求实数 a的值;
(2)利用单调性的定义证明函数f(x)在区间[1,+∞解析:(1)由f (1+x)=f (1-x)得,
(1+x)2+a(1+x)=(1-x)2+a(1-x),
整理得:(a+2)x=0,
由于对任意的x都成立,∴ a=-2. (7分)
(2)根据(1)可知 f ( x )=x 2-2x,下面证明函数f(x)在区间[1,+∞![]() 上是增函数.
上是增函数.
设![]() ,则
,则![]() =
=![]() -
-![]()
=(![]() )-2(
)-2(![]() )
)
=(![]() )(
)(![]() -2)
-2)
∵![]() ,则
,则![]() >0,且
>0,且![]() -2>2-2=0,
-2>2-2=0,
∴ ![]() >0,即
>0,即![]() ,
,
故函数f(x)在区间[1,+∞![]() 上是增函数. (8分)
上是增函数. (8分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (0,1),
(0,1), ,直线
,直线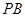 、
、 都是圆
都是圆 的切线(
的切线(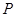 点不在
点不在 轴上).
轴上). 轴上的抛物线的标准方程;
轴上的抛物线的标准方程; 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使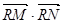 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由 ,命题q:
,命题q: . 若“p且q”为真命题,求实数m的取值范围.
. 若“p且q”为真命题,求实数m的取值范围. 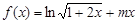 .
.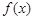 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围; 时,求函数
时,求函数 ,且
,且 时,证明:
时,证明: .
. 和抛物线C:
和抛物线C: ,圆的切线
,圆的切线 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B, 对称,问是否存在直线
对称,问是否存在直线 ?若存在,求出直线
?若存在,求出直线
 ,曲线
,曲线
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值; ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]