题目内容
(本题满分15分)已知点 (0,1),
(0,1), ,直线
,直线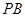 、
、 都是圆
都是圆 的切线(
的切线(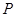 点不在
点不在 轴上).
轴上).
(Ⅰ)求过点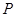 且焦点在
且焦点在 轴上的抛物线的标准方程;
轴上的抛物线的标准方程;
(Ⅱ)过点(1,0)作直线 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使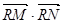 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由
(Ⅰ)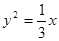 ;(Ⅱ)
;(Ⅱ)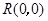 ,
,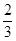 。
。
解析试题分析:(Ⅰ)设直线 的方程为:
的方程为: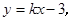
由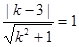 得
得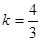 ,所以
,所以 的方程为
的方程为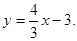 (4分)
(4分)
由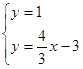 得
得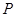 点的坐标为
点的坐标为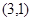 .
.
可求得抛物线的标准方程为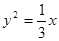 . (6分)
. (6分)
(Ⅱ)设直线 的方程为
的方程为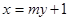 ,
,
代入抛物线方程并整理得 (8分)
(8分)
设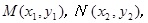 则
则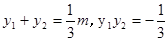
设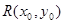 ,则
,则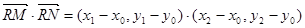
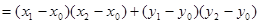
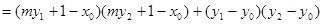
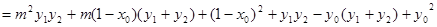
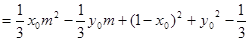 (12分)
(12分)
当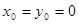 时上式是一个与
时上式是一个与 无关的常数.
无关的常数.
所以存在定点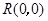 ,相应的常数是
,相应的常数是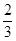 . (15分)
. (15分)
考点:本题考查直线与抛物线的综合问题;平面向量数量积的运算;抛物线的标准方程.
点评:本题主要考查了直线与抛物线的综合问题.研究直线与抛物线位置关系的问题,通常有两种方法:一是转化为研究方程组的解的问题,利用直线方程与抛物线方程所组成的方程组消去一个变量后,将交点问题(包括公共点个数、与交点坐标有关的问题)转化为一元二次方程根的问题,结合根与系数的关系及判别式解决问题;二是运用数形结合的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,命题q:
,命题q: . 若“p且q”为真命题,求实数m的取值范围.
. 若“p且q”为真命题,求实数m的取值范围. 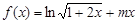 .
.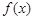 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围; 时,求函数
时,求函数 ,且
,且 时,证明:
时,证明: .
. 和抛物线C:
和抛物线C: ,圆的切线
,圆的切线 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B, 对称,问是否存在直线
对称,问是否存在直线 ?若存在,求出直线
?若存在,求出直线
 ,曲线
,曲线
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值; ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]