题目内容
(本题满分15分)已知函数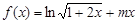 .
.
(Ⅰ)若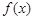 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;
(Ⅱ)当 时,求函数
时,求函数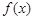 的最大值;
的最大值;
(Ⅲ)当 ,且
,且 时,证明:
时,证明: .
.
【答案】
解: (Ⅰ)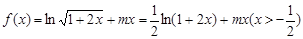 ,
,
∴ ---------2分
---------2分
若f(x)在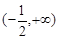 上是增函数,则
上是增函数,则 ,即
,即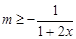 在
在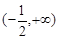 恒成立,
恒成立,
而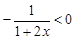 ,故m≥0;-----------------------------------------2分
,故m≥0;-----------------------------------------2分
若f(x)在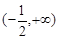 上是减函数,则
上是减函数,则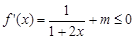 ,即
,即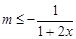 在
在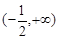 恒成立,
恒成立,
而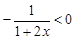 ,故这样的m不存在.------------------------------1分
,故这样的m不存在.------------------------------1分
经检验,当m≥0时,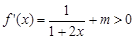 对
对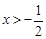 恒成立,
恒成立,
∴当m≥0时,f(x)在定义域上是单调增函数.---------------------1分
(Ⅱ)当m =-1时,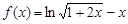 ,则
,则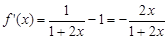 ----------1分
----------1分
当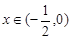 时,
时,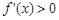 ,此时f(x)为增函数,
,此时f(x)为增函数,
当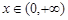 时,
时,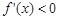 ,此时f(x)为减函数----------------------------2分
,此时f(x)为减函数----------------------------2分
∴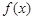 在x = 0时取得最大值,最大值为
在x = 0时取得最大值,最大值为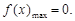 ----------------------1分
----------------------1分
(Ⅲ)当m = 1时,令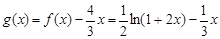 ,
, --1分
--1分
在[0,1]上总有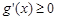 ,即
,即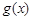 在[0,1]上递增------------------------------1分
在[0,1]上递增------------------------------1分
∴当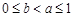 时,
时,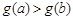 ,即
,即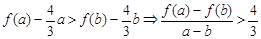 ----1分
----1分
令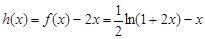 ,由(Ⅱ)知它在[0,1]上递减,所以当
,由(Ⅱ)知它在[0,1]上递减,所以当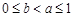 时,
时,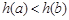 ,即
,即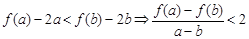 -----------------1分
-----------------1分
综上所述,当m = 1,且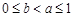 时,
时,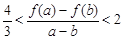 ---------------1分
---------------1分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (0,1),
(0,1), ,直线
,直线 、
、 都是圆
都是圆 的切线(
的切线(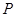 点不在
点不在 轴上).
轴上). 轴上的抛物线的标准方程;
轴上的抛物线的标准方程; 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使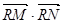 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由 ,命题q:
,命题q: . 若“p且q”为真命题,求实数m的取值范围.
. 若“p且q”为真命题,求实数m的取值范围.  和抛物线C:
和抛物线C: ,圆的切线
,圆的切线 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B, 对称,问是否存在直线
对称,问是否存在直线 ?若存在,求出直线
?若存在,求出直线
 ,曲线
,曲线
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值; ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]