题目内容
(本小题满分13分)
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF=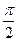 ,AD=
,AD=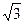 ,EF=2.
,EF=2.
(Ⅰ)求证: AE∥平面DCF;
(Ⅱ)若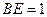 ,且二面角A—EF—C的大小为
,且二面角A—EF—C的大小为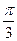 ,求
,求 的长。
的长。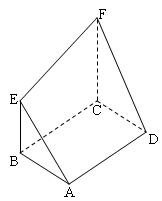
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF=
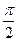 ,AD=
,AD=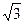 ,EF=2.
,EF=2.(Ⅰ)求证: AE∥平面DCF;
(Ⅱ)若
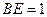 ,且二面角A—EF—C的大小为
,且二面角A—EF—C的大小为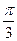 ,求
,求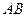 的长。
的长。
(Ⅰ)证明见解析。
(Ⅱ)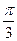
(Ⅱ)
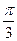
(Ⅰ)∵四边形ABCD是矩形,∴AB∥DC . …… 1分
又∵ BE∥CF , AB∩BE=B,
∴平面ABE∥平面DCF …… 3分
又AE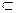 平面ABE,
平面ABE,
∴AE∥平面DCF……… 5分
(II)过E作GE⊥CF交CF于G,
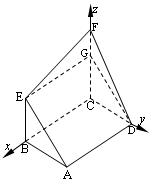
由已知 EG∥BC∥AD,且EG=BC=AD,
∴EG=AD=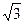 ,又EF=2,∴GF=1…6分
,又EF=2,∴GF=1…6分
∵四边形ABCD是矩形,∴DC⊥BC .
∵∠BCF=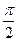 , ∴FC⊥BC,
, ∴FC⊥BC,
又平面AC⊥平面BF,平面AC∩平面BF=BC,
∴FC⊥平面AC ,∴FC⊥CD . …………7分
分别以CB、CD、CF为轴建立空间直角坐标系.
∵BE=1,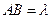 ,∴ A(
,∴ A(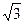 ,
,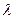 ,0),E(
,0),E(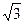 ,0,1),F(0,0,2),
,0,1),F(0,0,2),
∴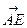 =(0,-
=(0,-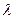 ,1),
,1),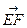 =(-
=(-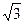 ,0,1). …………8分
,0,1). …………8分
设平面AEF的法向量 =(x,y,z),
=(x,y,z),
得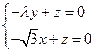 ,∴
,∴ ="("
="(" 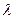 ,
,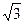 ,
,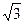
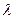 ). ……10分
). ……10分
又 =(0,
=(0,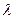 ,0)是平面CEF的一个法向量,
,0)是平面CEF的一个法向量,
∴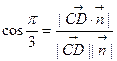 ,即
,即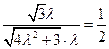 ,得
,得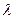 =
=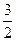 .
.
∴当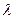 的值为
的值为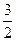 时,二面角A—EF—C的大小为
时,二面角A—EF—C的大小为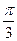 …13分
…13分
又∵ BE∥CF , AB∩BE=B,
∴平面ABE∥平面DCF …… 3分
又AE
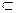 平面ABE,
平面ABE,∴AE∥平面DCF……… 5分
(II)过E作GE⊥CF交CF于G,

由已知 EG∥BC∥AD,且EG=BC=AD,
∴EG=AD=
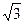 ,又EF=2,∴GF=1…6分
,又EF=2,∴GF=1…6分∵四边形ABCD是矩形,∴DC⊥BC .
∵∠BCF=
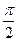 , ∴FC⊥BC,
, ∴FC⊥BC,又平面AC⊥平面BF,平面AC∩平面BF=BC,
∴FC⊥平面AC ,∴FC⊥CD . …………7分
分别以CB、CD、CF为轴建立空间直角坐标系.
∵BE=1,
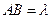 ,∴ A(
,∴ A(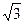 ,
,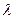 ,0),E(
,0),E(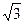 ,0,1),F(0,0,2),
,0,1),F(0,0,2),∴
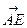 =(0,-
=(0,-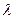 ,1),
,1),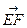 =(-
=(-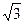 ,0,1). …………8分
,0,1). …………8分设平面AEF的法向量
 =(x,y,z),
=(x,y,z),得
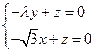 ,∴
,∴ ="("
="(" 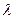 ,
,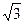 ,
,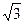
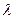 ). ……10分
). ……10分又
 =(0,
=(0,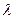 ,0)是平面CEF的一个法向量,
,0)是平面CEF的一个法向量,∴
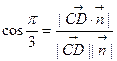 ,即
,即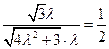 ,得
,得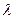 =
=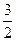 .
.∴当
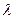 的值为
的值为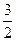 时,二面角A—EF—C的大小为
时,二面角A—EF—C的大小为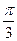 …13分
…13分

练习册系列答案
相关题目
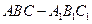 中,
中,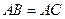 ,点
,点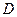 在边
在边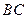 上,
上,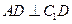 。
。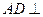 平面
平面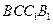 ;
;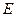 是
是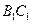 的中点,求证:
的中点,求证: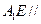 平面
平面 .
.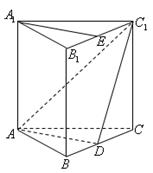
 的各棱长都为
的各棱长都为 ,
,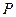 为棱
为棱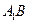 上的动点.
上的动点.
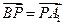 时,求证:
时,求证: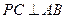 ;
; 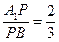 ,求二面角
,求二面角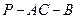 的大小;
的大小; 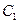 到平面
到平面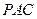 的距离.
的距离.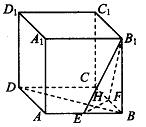
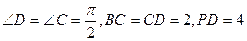 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将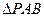 沿AB折到
沿AB折到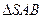 的位置,使
的位置,使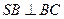 ,点E在SD上,且
,点E在SD上,且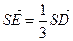 ,如下右图。
,如下右图。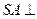 平面ABCD;
平面ABCD;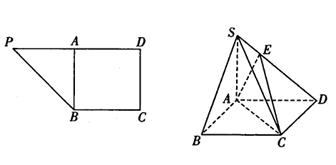 (2)求二面角E—AC—D的正切值;
(2)求二面角E—AC—D的正切值;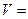 ( )
( )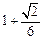
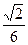
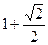
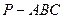 中,
中,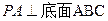 ,
,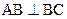 ,
,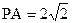 ,
,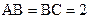 ,若
,若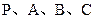 四点在同一个球面上,则在球面上
四点在同一个球面上,则在球面上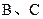 两点之间的球面距离是_____ .
两点之间的球面距离是_____ .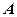 、
、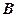 、
、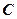 的截面与球心的距离为球半径的一半,且
的截面与球心的距离为球半径的一半,且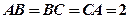 ,则这个球的表面积等于( )
,则这个球的表面积等于( )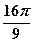
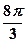
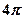
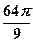
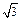 的正三棱锥
的正三棱锥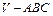 的外接球的球心为O,满足
的外接球的球心为O,满足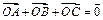 , 则该三棱锥外接球的体积为 .
, 则该三棱锥外接球的体积为 .