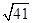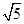题目内容
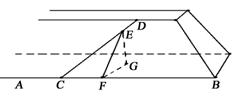
河堤斜面与水平面所成角为60°,堤面上有一条直道CD,它与堤角的水平线AB的夹角为30°,沿着这条直道从堤角向上行走到10米时,人升高了多少(精确到0.1米)?
已知 所求
河堤斜面与水平面所成角为60° E到地面的距离
利用E或G构造棱上一点F 以EG为边构造三角形
解:取CD上一点E,设CE=10 m,过点E作直线AB所在的水平面的垂线EG,垂足为G,则线段EG的长就是所求的高度.
在河堤斜面内,作EF⊥AB.垂足为F,连接FG,由三垂线定理的逆定理,知FG⊥AB.因此,∠EFG就是河堤斜面与水平面ABG所成的二面角的平面角,∠EFG=60°.
由此得:
EG=EFsin60°
=CE sin30°sin60°
=10× ×
×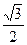 ≈4.3(m)
≈4.3(m)
答:沿着直道向上行走到10米时,人升高了约4.3米.


河堤斜面与水平面所成角为60° E到地面的距离
利用E或G构造棱上一点F 以EG为边构造三角形
解:取CD上一点E,设CE=10 m,过点E作直线AB所在的水平面的垂线EG,垂足为G,则线段EG的长就是所求的高度.
在河堤斜面内,作EF⊥AB.垂足为F,连接FG,由三垂线定理的逆定理,知FG⊥AB.因此,∠EFG就是河堤斜面与水平面ABG所成的二面角的平面角,∠EFG=60°.
由此得:
EG=EFsin60°
=CE sin30°sin60°
=10×
 ×
×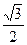 ≈4.3(m)
≈4.3(m)答:沿着直道向上行走到10米时,人升高了约4.3米.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目


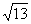 ,则P点坐标是( )
,则P点坐标是( ) 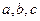 ,则长方体体对角线长为( )
,则长方体体对角线长为( )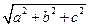
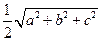
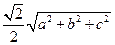
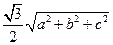
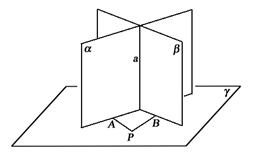
 所在的平面,
所在的平面,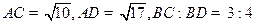 ,当
,当