题目内容
圆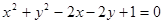
上的点到直线
的距离最大值是( )
| A．2 | B．1+ | C． | D．1+ |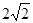
B
解析试题分析：因为圆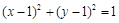
，而所求距离最大值为圆心到直线距离加半径，即
考点：直线与圆位置关系
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若直线
与圆
相切，且
为锐角，则这条直线的斜率是( )
A． | B． | C． | D． |
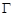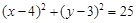已知圆
：
，过圆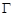内定点P（2，1）作两条相互垂直的弦AC和BD，那么四边形ABCD面积最大值为（ ）
| A．21 | B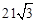． | C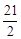． | D．42 |
已知
，则直线
与圆：
的位置关系是( )．
| A．相交 | B．相切 | C．相离 | D．不能确定 |
过点
的直线,将圆形区域
分两部分,使得这两部分的面积之差最大,则该直线的方程为（ ）
A． | B． | C． | D． |
过
的直线
被圆
截得的线段长为2时，直线的斜率为（ ）
A． | B． | C． | D． |
若圆O：x2＋y2＝4与圆C：x2＋y2＋4x－4y＋4＝0关于直线l对称，则直线l的方程是( )
| A．x＋y＝0 | B．x－y＝0 |
| C．x－y＋2＝0 | D．x＋y＋2＝0 |
－4
－1