题目内容
【题目】某小型餐馆一天中要购买![]() ,
,![]() 两种蔬菜,
两种蔬菜,![]() ,
,![]() 蔬菜每公斤的单价分别为2元和3元.根据需要
蔬菜每公斤的单价分别为2元和3元.根据需要![]() 蔬菜至少要买6公斤,
蔬菜至少要买6公斤,![]() 蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,
蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,![]() ,
,![]() 两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
【答案】应购买![]() 蔬菜
蔬菜![]() 公斤,
公斤,![]() 蔬菜
蔬菜![]() 公斤,加工后利润最大为
公斤,加工后利润最大为![]() 元.
元.
【解析】
试题分析:借助题设条件建立不等式组求解,运用线性规划的知识数形结合求解.
试题解析:
设餐馆一天购买![]() 蔬菜
蔬菜![]() 公斤,购买
公斤,购买![]() 蔬菜
蔬菜![]() 公斤,获得的利润为
公斤,获得的利润为![]() 元,依题意可知
元,依题意可知![]() ,
,![]() 满足的不等式组如下:
满足的不等式组如下: 目标函数为
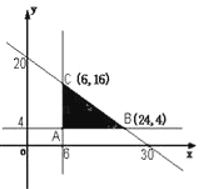
目标函数为![]() .画出的平面区域如图.
.画出的平面区域如图.
∵![]() ,∴表示
,∴表示![]() 过可行域内点斜率为
过可行域内点斜率为![]() 的一组平行线在
的一组平行线在![]() 轴上的截距.
轴上的截距.
联立![]() 解得
解得![]() 即
即![]() ,
,
∴当直线过点![]() 时,在
时,在![]() 轴上的截距最大,
轴上的截距最大,
即![]() .
.
答:餐馆应购买![]() 蔬菜24公斤,
蔬菜24公斤,![]() 蔬菜4公斤,加工后利润最大为52元.
蔬菜4公斤,加工后利润最大为52元.

练习册系列答案
相关题目
【题目】一汽车![]() 店新进
店新进![]() 三类轿车,每类轿车的数量如下表:
三类轿车,每类轿车的数量如下表:
类别 |
|
|
|
数量 | 4 | 3 | 2 |
同一类轿车完全相同,现准备提取一部分车去参加车展.
(1)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(2)若一次性提取4辆车,其中![]() 三种型号的车辆数分别记为
三种型号的车辆数分别记为![]() ,记
,记![]() 为
为![]() 的最大值,求
的最大值,求![]() 的分布列和数学期望.
的分布列和数学期望.
