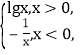题目内容
【题目】已知有限项的、正整数的递增数列![]() ,并满足如下条件:对任意不大于各项总和
,并满足如下条件:对任意不大于各项总和![]() 的正整数
的正整数![]() ,总存在一个子列,使得该子列所有项的和恰好等于
,总存在一个子列,使得该子列所有项的和恰好等于![]() .这里的‘子列’是指由原数列中的一部分项(包括一项、所有项)组成的新数列.
.这里的‘子列’是指由原数列中的一部分项(包括一项、所有项)组成的新数列.
(1)写出![]() ,
,![]() 的值;
的值;
(2)“![]() 成等差数列”的充要条件是“
成等差数列”的充要条件是“![]() 各项总和
各项总和![]() 恰好是其项数、项数平方值的等差中项”.为什么?请说明理由.
恰好是其项数、项数平方值的等差中项”.为什么?请说明理由.
(3)若![]() ,写出“
,写出“![]() 项数最少时,
项数最少时,![]() 中的最大项”的值.
中的最大项”的值.
【答案】(1)![]() ;(2)证明见解析;(3)当
;(2)证明见解析;(3)当![]() 取最小值
取最小值![]() 时,
时,![]() 的最大值为1010.
的最大值为1010.
【解析】
(1)利用数列是正整数的递增数列及题意可求;
(2)先利用等差数列求和公式证明必要性,再利用放缩法证明充分性;
(3)由题意可知,![]() 恒成立,由
恒成立,由![]() 可得
可得![]() ,由集合分类进行验证可得
,由集合分类进行验证可得![]() 的最大值.
的最大值.
(1)因为![]() ,且
,且![]() 是递增的正整数数列,由题意可知
是递增的正整数数列,由题意可知![]() .
.
(2)先证必要性:
因为![]() ,且
,且![]() 成等差数列,所以
成等差数列,所以![]() ,所以
,所以![]() .
.
再证充分性:
因为![]() 是递增的正整数数列,
是递增的正整数数列,![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() (
(![]() ),
),
故![]() 是等差数列.
是等差数列.
(3)先证明![]() 恒成立.
恒成立.
假设存在![]() ,且
,且![]() 为最小的正整数.
为最小的正整数.
依题意![]() ,则
,则![]() ,
,
又因为![]() ,故当
,故当![]() 时,
时,![]() 不能等于任何子列所有项的和.
不能等于任何子列所有项的和.
故假设不成立,即![]() 恒成立.
恒成立.
因此![]() ,即
,即![]() ,所以
,所以![]() .
.
因为![]() ,则
,则![]() ,
,
若![]() 时,则当
时,则当![]() 时,
时,![]() 不能等于任何子列所有项的和.
不能等于任何子列所有项的和.
故![]() ,即
,即![]() .
.
此时可构造集合![]() .
.
当![]() 时,
时,![]() 可以等于集合
可以等于集合![]() 中若干个元素的和;
中若干个元素的和;
当![]() 时,
时,![]() 可以等于集合
可以等于集合![]() 中若干个元素的和;
中若干个元素的和;
![]()
![]()
当![]() 时,
时,![]() 可以等于集合
可以等于集合![]() 中若干个元素的和;
中若干个元素的和;
当![]() 时,
时,![]() 可以等于集合
可以等于集合![]() 中若干个元素的和;
中若干个元素的和;
当![]() 时,
时,![]() 可以等于集合
可以等于集合![]() 中若干个元素的和;
中若干个元素的和;
所以当![]() 取最小值
取最小值![]() 时,
时,![]() 的最大值为1010.
的最大值为1010.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目