题目内容
已知:| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
分析:根据题意,先求出
2,
2,
•
的值,由
•
=0得到4k=(sinx-
)2-
,利用二次函数的性质求得4k的最值,即可得到实数k的值域.
| a |
| b |
| a |
| b |
| c |
| d |
| 3 |
| 2 |
| 9 |
| 4 |
解答:解:
2=4,
2=1,
•
=0,
由题意得
•
=(
+(sinx-3)
)•(-k
+sinx
)=-k
2+sinx
•
-k(sinx-3)
•
+sinx(sinx-3)
2
=-4k+0+0+sinx(sinx-3)=0,
∴4k=(sinx-
)2-
,
∴当sinx=1时,4k有最小值为-2,
当 sinx=-1时,4k有最大值为 4. 故 k 的最小值-
,k的最大值为1,
综上,实数k的取值范围为[-
,1].
| a |
| b |
| a |
| b |
由题意得
| c |
| d |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| b |
=-4k+0+0+sinx(sinx-3)=0,
∴4k=(sinx-
| 3 |
| 2 |
| 9 |
| 4 |
∴当sinx=1时,4k有最小值为-2,
当 sinx=-1时,4k有最大值为 4. 故 k 的最小值-
| 1 |
| 2 |
综上,实数k的取值范围为[-
| 1 |
| 2 |
点评:本题考查两个向量的数量积公式的应用,两个向量坐标形式的运算,以及二次函数的最值的求法.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
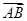 的坐标是( )
的坐标是( )