Question

【题目】正整数数列满足（p，q为常数），其中为数列的前n项和．

(1)若，，求证：是等差数列；

(2)若数列为等差数列，求p的值；

(3)证明：的充要条件是．

Answer 1

【答案】（1）证明见解析；（2）或；（3）证明见解析.

【解析】

（1），时，，可得，时，，化为：，即可证明.

（2）设等差数列的公差为，可得，.

又，可得.比较两边的系数可得：，对分类讨论，进而得出．

（3）由，可得．由，利用递推关系可得：，即.必要性：当时，可得.充分性：反证法，当时，可得，不满足.当时，同理可证明，不满足.

（1），时，，可得.

时，，

整理为：，

∴，∴是等差数列.

（2）设等差数列的公差为d，

∴，.

则，

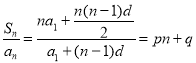∴①.

比较两边的系数可得：，

当时，，解得，．

此时，，由（1）可得：是等差数列.

当时，．由①比较常数项可得：，

则，，是等差数列.

综上可得：或.

（3）证明：由，可得.

由，

相减可得：，即．

必要性：当时，．

∴……，

∴.

充分性：反证法，当时，

由，

又数列各项为正数，

∴，即，

∴，不满足．当时，

同理可证明，不满足.