题目内容
已知△ABC中,a=4,b=4 , A=30°,则角B等于( )
, A=30°,则角B等于( )
| A.30° | B.30°或150° | C.60° | D.60°或120° |
D
解析试题分析:∵a=4,b=4 ,∠A=30°,
,∠A=30°,
∴根据正弦定理得: ,得到
,得到 又B为锐角,
又B为锐角,
则∠B=60°;故选D
考点:本题主要考查了正弦定理,等腰三角形的判定,以及特殊角的三角函数值.
点评:熟练掌握正弦定理是解本题的关键. 由A的度数求出sinA的值,再由a与b的值,利用正弦定理求出sinB的值,由B不可能为钝角或直角,得到B为锐角,利用特殊角的三角函数值即可求出B的度数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中,若b=6,c=10,B=30°,则解此三角形的结果为( )
| A.无解 | B.有一解 | C.有两解 | D.一解或两解 |
在 中,若
中,若 ,则
,则 的形状一定是( )
的形状一定是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等边三角形 |
已知△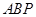 的顶点
的顶点 、
、 分别为双曲线
分别为双曲线 的左右焦点,顶点
的左右焦点,顶点 在双曲线
在双曲线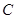 上,则
上,则 的值等于
的值等于
A. | B. | C. | D. |
在△ABC中,若 ,则∠A= ( )
,则∠A= ( )
A. | B. | C. | D.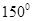 |
在 中,已知
中,已知 ,那么这个三角形一定是( )
,那么这个三角形一定是( )
| A.等边三角形 | B.直角三角形 |
| C.等腰三角形 | D.等腰直角三角形 |
在 中,
中, ,
, ,
, , 则三角形的面积为( )
, 则三角形的面积为( )
A. | B.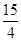 | C. | D. |
 B.
B. C.
C. D.
D.
 中,∠A、∠B的对边分别为a,b,且∠A=60°,
中,∠A、∠B的对边分别为a,b,且∠A=60°, ,那么满足条件的
,那么满足条件的