题目内容
【题目】圆M：x2+y2﹣2y=24，直线l：x+y=11，l上一点A的横坐标为a，过点A作圆M的两条切线l1 ， l2 ， 切点为B，C．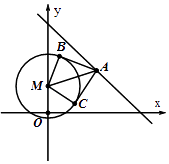 
（1）当a=0时，求直线l1 ， l2的方程；
（2）是否存在点A，使得 
=﹣2？若存在，求出点A的坐标，若不存在，请说明理由．
（3）求证当点A在直线l运动时，直线BC过定点P0 ．
（附加题）问：第（3）问的逆命题是否成立？
【答案】
（1）解：圆M：x2+（y﹣1）2=25，圆心M（0，1），半径r=5，A（0，11），
设切线的方程为y=k x+11，圆心距d= 
=5，
∴k=± 
，所求直线l1，l2的方程为y=± x+11
（2）解：当l1⊥l2时，四边形MCAB为正方形，
∴|AM|+ 
|MB|=5
设A（a，11﹣a），M（0，1）则 
= 
a2﹣10a+25=0∴a=5
设 
=2θ，则
=|AB|2（1﹣2sin2θ），
又sinθ= 
，故 =（AM2﹣25）（1﹣ 
）=AM2+ 
﹣75，
又圆心M到直线l的距离是
∴AM2≥50， ≥50+ 
﹣75=0，故点A不存在．
（3）解：设A（a，b），则a+b=1 ①；
已AM为直径的圆与圆M交于B，C，AB，AC为切线；
以AM为直径的圆方程为：x（x﹣a）+（y﹣1）（y﹣b）=0 ②
圆M：x2+y2﹣2y=24 ③，
两式②③相减得公共弦BC方程：24+2y﹣ax﹣（b+1）y+b=0，代入①化简：
y﹣ 
=﹣ 
（x﹣ 
），故知P0 （ ， ）．
附加题：
首先：第（3）的逆命题是：过定点P0 （ ， ）的直线交圆x2+y2﹣2y=24 于B．C两点，分别以B，C为切点作圆M的切线l1，l2 相交于A点，则A在x+y=11上．
证明：设A（a，b），已AM为直径的圆与圆M交于B，C，易证AB，AC为切线；
以AM为直径的圆方程为：x（x﹣a）+（y﹣1）（y﹣b）=0
圆M：x2+y2﹣2y=24，
两式相减得公共弦BC方程：24+2y﹣ax﹣（b+1）y+b=0，
由于公共弦BC所在直线过定点P0 （ ， ），代入可得a+b=11，得证
【解析】（1）利用点到直线的距离公式，可直接求出斜率；（2）当l1⊥l2时，四边形MCAB为正方形，求出a的值；设 =2θ，则 =|AB|2（1﹣2sin2θ），故 =（AM2﹣25）（1﹣ ）=AM2+ ﹣75，又圆心M到直线l的距离是 ∴AM2≥50， ≥50+ ﹣75=0，故点A不存在．（3）利用两圆方程相减，求出公共弦直线方程，找出定点．
