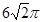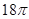题目内容
(本小题满分12分)
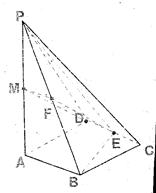
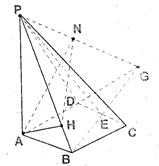
如图,四棱锥P—ABCD的底面ABCD是 边长为2的菱形,
边长为2的菱形,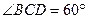 ,E是CD的中点,PA
,E是CD的中点,PA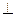 底面ABC
底面ABC D,PA=4
D,PA=4
(1)证明:若F是棱PB的中点,求证:EF//平面PAD;
(2)求平面PAD和平面PBE所成二面角(锐角)的大小。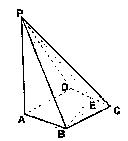
如图,四棱锥P—ABCD的底面ABCD是
 边长为2的菱形,
边长为2的菱形,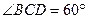 ,E是CD的中点,PA
,E是CD的中点,PA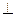 底面ABC
底面ABC D,PA=4
D,PA=4(1)证明:若F是棱PB的中点,求证:EF//平面PAD;
(2)求平面PAD和平面PBE所成二面角(锐角)的大小。

(1)略(2)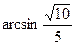
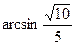
证明:(1)∵四边形ABCD是菱形,E是CD的中点
 ∴BE⊥AB,
∴BE⊥AB,
又PA⊥底面ABCD,
∴BE⊥PA
∴BE⊥平面PAB
∴BE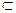 平面PBE
平面PBE
∴平面PBE⊥平面PAB
(2)设PA的中点为M,连接EF、FM、MD
则M F//
F//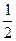 AB、DE//
AB、DE//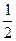 AB,
AB,
∴DE//FM、DE=FM
∴四边形EFMD是平面四边形,
∴EF//DM
又EF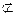 平面PAD,DM
平面PAD,DM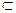 平面PAD
平面PAD
∴EF//平面PAD
(3)延长BE交AD的延长线于G,则PG是平面PAD和平面PBE的交线过点A作AH⊥OB、AN⊥PG,
∵AH⊥平面PAB,
∴∠ANH是平面PAD和平面PBE所成二面角的平面角
 在Rt△PAB中,PA=4、AB=2
在Rt△PAB中,PA=4、AB=2
∴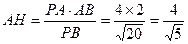
∵E是DC的中点,且AB//CD,
∴AG=2AD=4
∴在Rt△PAG中 ,AN=
,AN=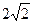 ,
,
∴Rt△ANH中,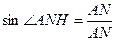
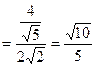
∴平面PAD和平面PBE所成 二面角的大小为
二面角的大小为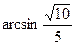
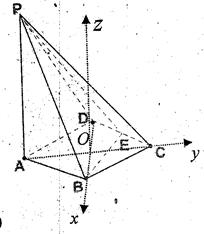
或如图,建立空间直角坐标系O—xyz,
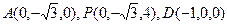
B(1,0,0),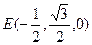
则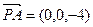 ,
,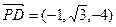
设平面PAD的法向量为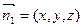
则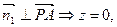
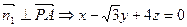
可得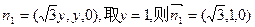
又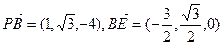
设平面PBE的法向量为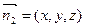
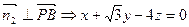 ,
,
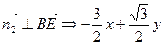 =0
=0
可得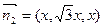 ,取x=1,
,取x=1,
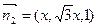
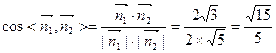
平 面PA
面PA D和平面PBE所成二面角的大小为
D和平面PBE所成二面角的大小为
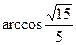
 ∴BE⊥AB,
∴BE⊥AB,又PA⊥底面ABCD,
∴BE⊥PA
∴BE⊥平面PAB
∴BE
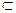 平面PBE
平面PBE∴平面PBE⊥平面PAB
(2)设PA的中点为M,连接EF、FM、MD
则M
 F//
F//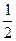 AB、DE//
AB、DE//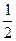 AB,
AB,∴DE//FM、DE=FM
∴四边形EFMD是平面四边形,
∴EF//DM
又EF
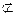 平面PAD,DM
平面PAD,DM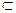 平面PAD
平面PAD∴EF//平面PAD
(3)延长BE交AD的延长线于G,则PG是平面PAD和平面PBE的交线过点A作AH⊥OB、AN⊥PG,
∵AH⊥平面PAB,
∴∠ANH是平面PAD和平面PBE所成二面角的平面角
 在Rt△PAB中,PA=4、AB=2
在Rt△PAB中,PA=4、AB=2∴
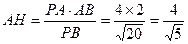
∵E是DC的中点,且AB//CD,
∴AG=2AD=4
∴在Rt△PAG中
 ,AN=
,AN=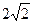 ,
,∴Rt△ANH中,
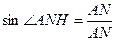

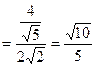
∴平面PAD和平面PBE所成
 二面角的大小为
二面角的大小为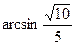
或如图,建立空间直角坐标系O—xyz,
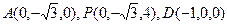
B(1,0,0),
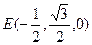
则
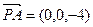 ,
,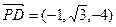
设平面PAD的法向量为
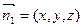
则
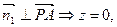
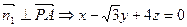
可得
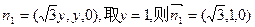
又
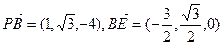
设平面PBE的法向量为
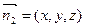
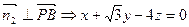 ,
,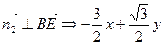 =0
=0可得
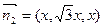 ,取x=1,
,取x=1,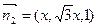
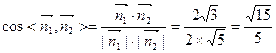
平
 面PA
面PA D和平面PBE所成二面角的大小为
D和平面PBE所成二面角的大小为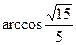

练习册系列答案
相关题目
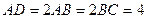 ,
,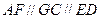 且
且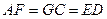 ,
, ,
,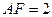 ,H是棱EF的中点
,H是棱EF的中点







 (1)证明:平面
(1)证明:平面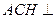 平面CDE;
平面CDE;
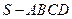 的底面是正方形,每条侧棱长都是底面边长的
的底面是正方形,每条侧棱长都是底面边长的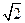 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。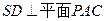 ,求二面角
,求二面角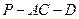 的大小;
的大小;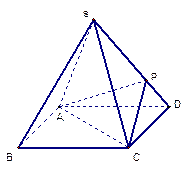
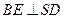 ,若存在,求
,若存在,求 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。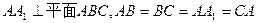 ,
,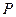 为
为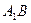 上的点.
上的点.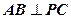 ;
;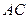 —
—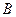 的大小为
的大小为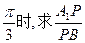 的值.
的值.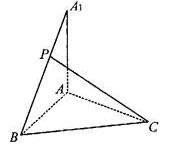
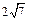 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点,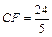 ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.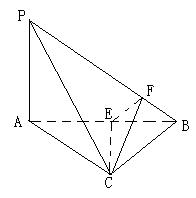
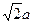 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.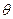 的大小.
的大小. 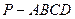 的底面
的底面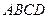 不是平行四边形,用平面
不是平行四边形,用平面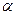 去截此四棱锥,使得截面四边形是平行四边形,则这样的平面
去截此四棱锥,使得截面四边形是平行四边形,则这样的平面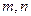 为两条不同的直线,
为两条不同的直线,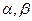 为两个不同的平面,给定下列条件:
为两个不同的平面,给定下列条件: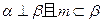 ;②
;②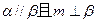 ;③
;③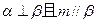 ;④
;④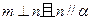 .其中可以判定
.其中可以判定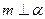 的有 ( )
的有 ( )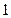 个
个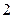 个
个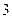 个
个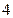 个
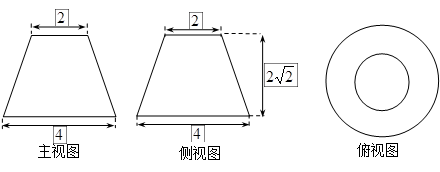
个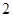 ,下底为
,下底为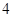 ,高为
,高为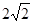 的等腰梯形,俯视图是两个半径分别为
的等腰梯形,俯视图是两个半径分别为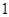 和
和