题目内容
函数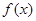 =
=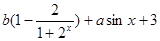 (
(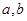 为常数),若f(x)在(0,+∞)上有最大值10,则
为常数),若f(x)在(0,+∞)上有最大值10,则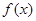 在
在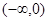 上有( )
上有( )
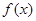 =
=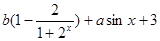 (
(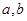 为常数),若f(x)在(0,+∞)上有最大值10,则
为常数),若f(x)在(0,+∞)上有最大值10,则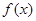 在
在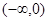 上有( )
上有( )| A.最大值10 | B.最小值-5 | C.最小值-4 | D.最大值9 |
C
分析:函数变形为g(x)=f(x)-3,判断函数g(x)的奇偶性,利用f(x)在(0,+∞)上有最大值10,求出f(x)在(-∞,0)上有最小值,即可.
解答:解:函数f(x)=b(1-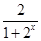 )+asinx+3(a,b为常数),
)+asinx+3(a,b为常数),
化为g(x)=f(x)-3=b(1-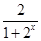 )+asinx,
)+asinx,
因为g(-x)=b(1-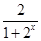 )+asin(-x)=-[b(1-
)+asin(-x)=-[b(1-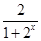 )+asinx]=-g(x),
)+asinx]=-g(x),
所以函数g(x)是奇函数,f(x)在(0,+∞)上有最大值10,所以g(x)在(0,+∞)上有最大值7,
g(x)在(-∞,0)上有最小值-7,所以f(x)在(-∞,0)上有最小值-7+3=-4.
故选C.
解答:解:函数f(x)=b(1-
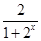 )+asinx+3(a,b为常数),
)+asinx+3(a,b为常数),化为g(x)=f(x)-3=b(1-
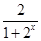 )+asinx,
)+asinx,因为g(-x)=b(1-
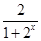 )+asin(-x)=-[b(1-
)+asin(-x)=-[b(1-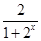 )+asinx]=-g(x),
)+asinx]=-g(x),所以函数g(x)是奇函数,f(x)在(0,+∞)上有最大值10,所以g(x)在(0,+∞)上有最大值7,
g(x)在(-∞,0)上有最小值-7,所以f(x)在(-∞,0)上有最小值-7+3=-4.
故选C.

练习册系列答案
相关题目
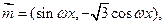
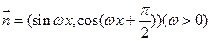 ,若函数
,若函数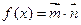 的最小正周期为
的最小正周期为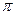
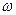 的值
的值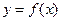 的图象向右平移
的图象向右平移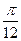 个单位,再将所得到的图象上各点的横坐标伸长到原来的
个单位,再将所得到的图象上各点的横坐标伸长到原来的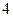 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数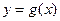 的图象,求
的图象,求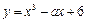 的一个单调增区间为
的一个单调增区间为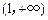 ,求
,求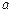 的值及函数的其他单调区间.
的值及函数的其他单调区间.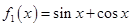 ,
,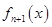 是
是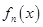 的导函数,即
的导函数,即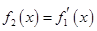 ,
,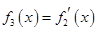 ,…,
,…,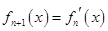 ,
,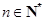 ,则
,则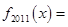 ( )
( )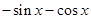
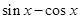
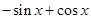
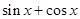
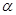 为第一象限角是
为第一象限角是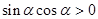 的 ( )
的 ( )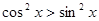 的解集为( )
的解集为( )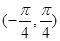
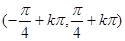
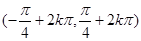
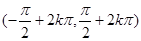 以上
以上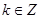
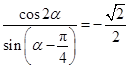 ,则
,则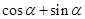 的值为( )
的值为( )
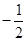


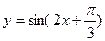 先向右平移
先向右平移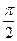 个单位,然后向下平移2个单位后所得的
个单位,然后向下平移2个单位后所得的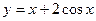 在
在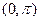 上的单调递减区间为 .
上的单调递减区间为 .