题目内容
已知函数
(1)判断函数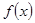 的单调性并用函数单调性定义加以证明;
的单调性并用函数单调性定义加以证明;
(2)若 在
在 上的值域是
上的值域是 ,求
,求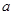 的值;
的值;
(3)当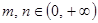 ,若
,若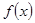 在
在 上的值域是
上的值域是
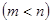 ,求实数
,求实数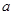 的取值范围.
的取值范围.
【答案】
(1)根据函数单调性定义可以证明函数是单调递增的(2)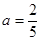 (3)
(3)
【解析】
试题分析:(1)设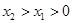 ,则
,则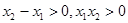 ,
,

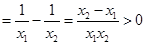 ,
,
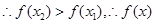 在
在 上是单调递增的. ……4分
上是单调递增的. ……4分
(2)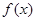 在
在 上单调递增,
上单调递增, ,易得
,易得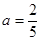 .
……8分
.
……8分
(3) 依题意得 ,
,
又 方程
方程 有两个不等正实数根
有两个不等正实数根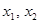 ,
,
又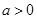 ,对称轴
,对称轴 ,
,
∴实数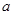 的取值范围为
的取值范围为 . ……14分
. ……14分
注意:利用对勾函数求出答案同样给分.
考点:本小题主要考查函数单调性的判断和证明、利用函数的单调性求参数和参数的取值范围,考查学生综合应用函数的性质解决问题的能力.
点评:证明函数的单调性要严格按照定义来证明,求参数或参数的取值范围时要适当转化问题.

练习册系列答案
相关题目
 .
. 在定义域上的单调性;
在定义域上的单调性; 在
在 上恒成立时的实数
上恒成立时的实数 的取值范围?
的取值范围? .
.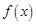 的奇偶性;
的奇偶性;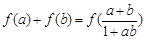 ;
; ,
, ,求
,求 ,
, 的值.
的值. .
. 在
在 上的单调性,不用证明;
上的单调性,不用证明; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; 上的值域是
上的值域是 ,求实数
,求实数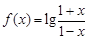 .
. 的奇偶性;
的奇偶性; ;
; ,
, ,求
,求 ,
, 的值.
的值.