题目内容
(本小题满分12分)
已知函数 .
.
(1)判断函数 在定义域上的单调性;
在定义域上的单调性;
(2)利用题(1)的结论,,求使不等式 在
在 上恒成立时的实数
上恒成立时的实数 的取值范围?
的取值范围?
【答案】
(1) 在
在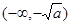 ,
,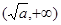 上是增函数,在
上是增函数,在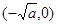 ,
, 上是减函数.
上是减函数.
(2) .
.
【解析】
试题分析:(1)法一:用单调性定义可解.
法二: ,
,
当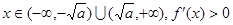 ;
; .……4分
.……4分
所以 在
在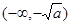 ,
,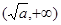 上是增函数,在
上是增函数,在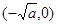 ,
, 上是减函数.…5分
上是减函数.…5分
(2)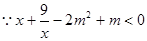 在
在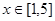 上恒成立,
上恒成立,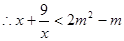 在
在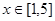 上恒成立,
上恒成立,
由(1)中结论可知,函数 在
在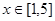 上的最大值为10,此时
上的最大值为10,此时 .
.
要使原命题成立,当且仅当 ,
, ,解得
,解得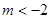 或
或 ,…11分
,…11分
 实数
实数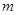 的取值范围是
的取值范围是 .
.
考点:本题主要考查应用导数研究函数的单调性及极值,简单不等式解法。
点评:典型题,本题属于导数应用中的基本问题,(2)作为 “恒成立问题”,转化成求函数最值问题。由本题看“对号函数”的性质值得关注。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目