题目内容
9.已知数列{an},其前n项和为Sn,且an=-2[n-(-1)n],则S10=-110.分析 由通项公式和符号数列(-1)n,有奇数为负,偶数为正的特点,结合等差数列的求和公式,计算即可得到所求.
解答 解:由an=-2[n-(-1)n],
则S10=-2[(1+1)+(2-1)+(3+1)+(4-1)+(5+1)+…+(9+1)+(10-1)]
=-2×$\frac{1}{2}$×(1+10)×10=-110.
故答案为:-110.
点评 本题考查数列的求和,注意运用(-1)n,有奇数为负,偶数为正,同时考查等差数列的求和公式,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
19.已知[0,3]是函数f(x)定义域内的一个区间,若f(1)<f(2),则函数f(x)在区间[0,3]上是( )
| A. | 是增函数 | B. | 是减函数 | ||
| C. | 既是增函数又是减函数 | D. | 单调性不确定 |
14.已知θ是第四象限角,则sin(sinθ)( )
| A. | 大于0 | B. | 大于等于0 | C. | 小于0 | D. | 小于等于0 |
1.已知m>0,且10x=lg10m+lg$\frac{1}{m}$,则x的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
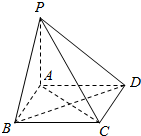 如图所示,四边形ABCD为正方形,PA⊥平面ABCD,则在平面PAB,平面PAD,平面PCD,平面PBC及平面ABCD中,互相垂直的有( )
如图所示,四边形ABCD为正方形,PA⊥平面ABCD,则在平面PAB,平面PAD,平面PCD,平面PBC及平面ABCD中,互相垂直的有( )