题目内容
(2012•济南二模)如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
AP=2,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将△PCD沿CD折起,使得PD⊥平面ABCD.

(1)求证:平面PCD⊥平面PAD;
(2)求二面角G-EF-D的大小;
(3)求三棱椎D-PAB的体积.
| 1 | 2 |

(1)求证:平面PCD⊥平面PAD;
(2)求二面角G-EF-D的大小;
(3)求三棱椎D-PAB的体积.
分析:(1)由PD⊥平面ABCD,可得PD⊥CD,根据CD⊥AD,可得CD⊥平面PAD,利用面面垂直的判定,可得平面PCD⊥平面PAD;
(2)建立空间直角坐标系,求出平面EFG的法向量
=(1,0,1),平面PCD的一个法向量
=(1,0,0),利用向量的夹角公式,可得二面角G-EF-D的平面角;
(3)利用等体积转化,可求三棱椎D-PAB的体积.
(2)建立空间直角坐标系,求出平面EFG的法向量
| n |
| DA |
(3)利用等体积转化,可求三棱椎D-PAB的体积.
解答: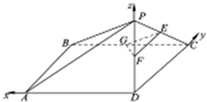 (1)证明:∵PD⊥平面ABCD,CD?平面ABCD,
(1)证明:∵PD⊥平面ABCD,CD?平面ABCD,
∴PD⊥CD…(1分)
∵CD⊥AD,PD∩AD=D
∴CD⊥平面PAD…(2分)
∵CD?平面PCD
∴平面PCD⊥平面PAD…(3分)
(2)解:如图以D为原点,以
,
,
为方向向量建立空间直角坐标系D-xyz,则G(1,2,0),E(0,1,1),F(0,0,1)
=(0,-1,0),
=(1,1,-1)…(5分)
设平面EFG的法向量为
=(x,y,z)
∴
,∴
,∴
.
取
=(1,0,1)…(6分)
平面PCD的一个法向量,
=(2,0,0)…(7分)
∴cos<
,
>=
=
=
…(8分)
结合图知二面角G-EF-D的平面角为45°…(9分)
(3)解:VD-PAB=VP-DAB=
S△ABD•PD=
×
×2×2×2=
…(12分)
 (1)证明:∵PD⊥平面ABCD,CD?平面ABCD,
(1)证明:∵PD⊥平面ABCD,CD?平面ABCD,∴PD⊥CD…(1分)
∵CD⊥AD,PD∩AD=D
∴CD⊥平面PAD…(2分)
∵CD?平面PCD
∴平面PCD⊥平面PAD…(3分)
(2)解:如图以D为原点,以
| DA |
| DC |
| DP |
| EF |
| EG |
设平面EFG的法向量为
| n |
∴
|
|
|
取
| n |
平面PCD的一个法向量,
| DA |
∴cos<
| DA |
| n |
| ||||
|
|
| 2 | ||
2
|
| ||
| 2 |
结合图知二面角G-EF-D的平面角为45°…(9分)
(3)解:VD-PAB=VP-DAB=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
点评:本题考查面面垂直,考查面面角,考查三棱锥体积的计算,解题的关键是掌握面面垂直的判定定理,正确运用空间向量解决面面角问题,属于中档题.

练习册系列答案
相关题目