题目内容

11．设函数f（x）的定义域为（0，+∞），且f（1）=0，若不等式$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0成立，则f（x）＞0的解集是（　　）
A．（0，+∞）B．（1，+∞）C．（0，1）D．（0，1）∪（1，+∞）

分析 根据不等式$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0成立，可判断函数为增函数，由f（1）=0，得出x的范围．

解答 解：$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0成立
∴f（x）在定义域内单调递增
f（x）＞0=f（1）
∴x＞1
故选B

点评 考察单调性的定义，基础题型

练习册系列答案
相关题目
17．试用描述法写出坐标系中下列点的集合．
（1）第一象限的点；
（2）x轴上方的点；
（3）坐标轴上的点；
（4）第一、三象限的点．
2．分解因式：8a3-b3．
19．已知2y•logy4-2y-1=0，2（logx5）2+logx$\frac{1}{5}$-1=0，当0＜x＜1时，求（xy）${\;}^{\frac{1}{2}}$的值．
6．已知x，y，z为正数，3x=4y=12z．
（1）若z=1，求$\frac{1}{x}$+$\frac{1}{y}$的值；
（2）证明：5z＜3x＜4y．
16．已知3sinβ=sin（2α+β），α≠kπ+$\frac{π}{2}$，α+β≠kπ+$\frac{π}{2}$（k∈Z），求证：tan（α+β）=2tanα
3．求函数y=$\sqrt{{5}^{x}-25}$的定义域，最小值，并求取得最小值时，自变量x的取值范围．
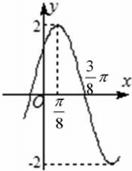20．函数f（x）=2sin（ωx+φ），（ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示，
（1）求ω，φ的值；
（2）在△ABC中，角A，B，C的对边分别为a，b，c，a=$\sqrt{2}$，b=1，f（$\frac{A}{2}$）=2，求角B的值．
1．已知f（x）=$\left\{\begin{array}{l}{3x+2，x＜1}\\{x+a，x≥1}\end{array}\right.$，若f（f（10））=4a，则实数a=5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网