题目内容
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 所在的平面和圆
所在的平面和圆![]() 所在的平面互相垂直,且
所在的平面互相垂直,且![]() .
.
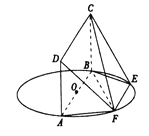
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求几何体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)利用面面垂直的性质定理可知![]() ,由圆的性质可得
,由圆的性质可得![]() ,则
,则![]() 平面
平面![]() ,最后利用面面垂直的判断定理可得平面
,最后利用面面垂直的判断定理可得平面![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 于
于![]() ,将几何体分解为一个三棱锥和一个四棱锥,计算可得四棱锥的体积
,将几何体分解为一个三棱锥和一个四棱锥,计算可得四棱锥的体积![]() ,三棱锥的体积
,三棱锥的体积![]() ,而FG的长度等于边长为1的等边三角形OEF的高,即
,而FG的长度等于边长为1的等边三角形OEF的高,即![]() ,据此计算可得几何体
,据此计算可得几何体![]() 的体积是
的体积是![]() .
.
试题解析:
(1)证明:由平面![]() 平面
平面![]() ,
, ![]() ,
,
平面![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() 为圆
为圆![]() 的直径,所以
的直径,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 于
于![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
,
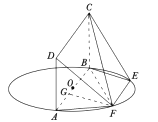
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]()
![]() .
.
连接![]() .∵
.∵![]() ,且
,且![]() .
.
∴![]() 为等边三角形,∴
为等边三角形,∴![]() .
.
∴几何体![]() 体积
体积![]() .
.

练习册系列答案
相关题目
【题目】下表是高三某位文科生连续5次月考的历史、政治的成绩,结果统计如下:
月份 | 9 | 10 | 11 | 12 | 1 |
历史(x分) | 79 | 81 | 83 | 85 | 87 |
政治(y分) | 77 | 79 | 79 | 82 | 83 |
(1)求该生5次月考历史成绩的平均分和政治成绩的方差
(2)一般来说,学生的历史成绩与政治成绩有较强的线性相关,根据上表提供的数据,求两个变量x、y的线性回归方程 ![]() =
= ![]() x+
x+ ![]()
(附: ![]() =
=  =
=  ,
, ![]() =y﹣
=y﹣ ![]() x)
x)

