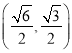Question

【题目】已知是整数，幂函数在上是单调递增函数.

(1)求幂函数的解析式；

(2)作出函数的大致图象；

(3)写出的单调区间，并用定义法证明在区间上的单调性.

Answer 1

【答案】(1)；(2)图象见解析；(3)减区间为；增区间为，证明见解析.

【解析】

(1)根据幂函数在上是单调递增函数，可知，解不等式即可.

(2)由(1)可知，则，先画出的图象，再将该图象轴下方的部分翻折到轴上方，即可.

(3)根据(2)的图象写出单调区间，再根据定义法证明函数单调性，即可.

(1)由题意可知，，即

因为是整数，所以或

当时，

当时，

综上所述，幂函数的解析式为.

(2) 由(1)可知，则

函数的图象，如图所示：

(3)由(2)可知，减区间为；增区间为

当时，

设任意的，且

则

又，且

即在区间上单调递增.