题目内容
已知椭圆C的方程为![]() ,双曲线
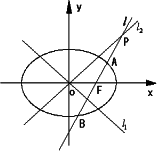
,双曲线![]() 的两条渐近线为l1,l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P,设l与椭圆C的两个交点由上至下依次为A、B(如图).
的两条渐近线为l1,l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P,设l与椭圆C的两个交点由上至下依次为A、B(如图).
(1)当l1与l2的夹角为60°,且△POF的面积为![]() 时,求椭圆C的方程;
时,求椭圆C的方程;
(2)当![]() 时,求
时,求![]() 的最大值.
的最大值.
答案:
解析:
提示:
解析:
解:(1)l1的斜率为![]() ,l2的斜率为
,l2的斜率为![]() ,由l1与l2的夹角为60°,得
,由l1与l2的夹角为60°,得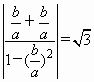 .
.
整理,得![]() .①
.①
由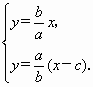 得
得![]() .由
.由![]() ,得
,得![]() .
.
∴![]() .②
.②
由①②,解得![]() ,b=1.∴椭圆C方程为:
,b=1.∴椭圆C方程为:![]() .
.
(2)由![]() ,F(c,0)及
,F(c,0)及![]() ,得
,得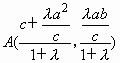 .
.
将A点坐标代入椭圆方程,得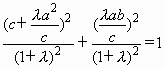 .
.
整理,得![]() ,
,
∴![]() 的最大值为
的最大值为![]() ,此时
,此时![]() .
.
提示:
分析:(1)求椭圆方程即求a、b.根据题中的两个数量关系:l1与l2的夹角为60°,△POF的面积为![]() ,列出关于a、b的两个方程即可.
,列出关于a、b的两个方程即可.
(2)由P、F的坐标求出A点的坐标,代入椭圆方程可得![]() 与a、b、c的关系,进而得出
与a、b、c的关系,进而得出![]() 与离心率e的关系.
与离心率e的关系.
说明:本题考查综合运用解析几何知识解决问题的能力,重点考查在圆锥曲线中解决问题的基本方法,转化能力,以及字母运算的能力.

练习册系列答案
相关题目