题目内容
求函数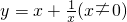
的最值．
解：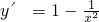
，
当0＜x＜1时，y′＜0，函数单调递减，当x＞1时，y′＞0，函数单调递增；
当x＜-1时，y′＞0，函数单调递增，-1＜x＜0时，y′＜0，函数单调递减；
所以函数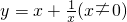在（-∞，-1）上递增，在（-1，0）上递减，在（0，1）上递减，在（1，+∞）上递增，
所以y=x+
≤-1+
=-2，或y=x+≥1+
=2，
故函数的值域为（-∞，-2]∪[2，+∞）．
故函数无最大值，也无最小值．
分析：求导数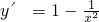，通过解不等式y′＞0，y′＜0可得函数的单调区间，由单调性可得结论．
点评：本题考查函数单调性的判断及证明，考查函数思想，属中档题．
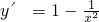，当0＜x＜1时，y′＜0，函数单调递减，当x＞1时，y′＞0，函数单调递增；
当x＜-1时，y′＞0，函数单调递增，-1＜x＜0时，y′＜0，函数单调递减；
所以函数
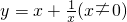在（-∞，-1）上递增，在（-1，0）上递减，在（0，1）上递减，在（1，+∞）上递增，所以y=x+
≤-1+=-2，或y=x+≥1+=2，故函数的值域为（-∞，-2]∪[2，+∞）．
故函数无最大值，也无最小值．
分析：求导数
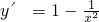，通过解不等式y′＞0，y′＜0可得函数的单调区间，由单调性可得结论．点评：本题考查函数单调性的判断及证明，考查函数思想，属中档题．
练习册系列答案
相关题目
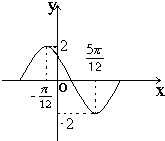已知函数y=Asin（ωx+?），x∈R（其中A＞0，ω＞0，0＜φ＜π）在一个周期内的图象如图，