题目内容
设a≥0,函数f(x)=[x2+(a-3)x-2a+3]ex,g(x)=2-a-x-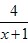 。
。
(I)当a≥1时,求f(x)的最小值;
(II)假设存在x1,x2∈(0,+∞),使得|f(x1)-g(x2)|<1成立,求a的取值范围。
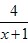 。
。(I)当a≥1时,求f(x)的最小值;
(II)假设存在x1,x2∈(0,+∞),使得|f(x1)-g(x2)|<1成立,求a的取值范围。
解:(Ⅰ)∵ ,
,
∵ ,
,
∴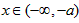 时,f(x)递增,
时,f(x)递增,
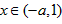 时,f(x)递减,
时,f(x)递减,
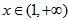 时,f(x)递增,
时,f(x)递增,
所以f(1)的极大值点为x1=-a,极小值点为x2=1,
而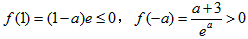 ,
,
由于,对二次函数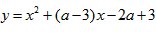 ,对称轴为
,对称轴为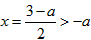 ,
, ,
,
∴当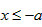 时,
时,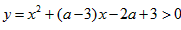 ,
,
∴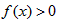 ,
,
当x>-a时,f(x)的最小值为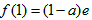 ,
,
所以,f(x)的最小值是 ;
;
(II)由(Ⅰ)知f(x)在的值域是:
当a≥1时,为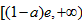 ,当
,当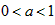 时,为
时,为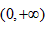 ;
;
而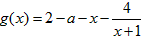 在
在 的值域是为
的值域是为 ,
,
所以,当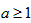 时,令
时,令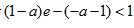 ,并解得
,并解得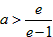 ,
,
当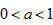 时,令
时,令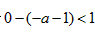 ,无解,
,无解,
因此,a的取值范围是 。
。
 ,
,∵
 ,
, ∴
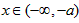 时,f(x)递增,
时,f(x)递增,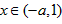 时,f(x)递减,
时,f(x)递减,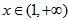 时,f(x)递增,
时,f(x)递增,所以f(1)的极大值点为x1=-a,极小值点为x2=1,
而
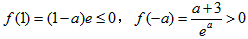 ,
,由于,对二次函数
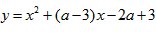 ,对称轴为
,对称轴为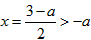 ,
, ,
, ∴当
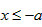 时,
时,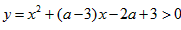 ,
,∴
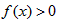 ,
,当x>-a时,f(x)的最小值为
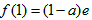 ,
,所以,f(x)的最小值是
 ;
;(II)由(Ⅰ)知f(x)在的值域是:
当a≥1时,为
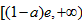 ,当
,当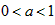 时,为
时,为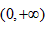 ;
;而
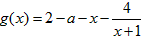 在
在 的值域是为
的值域是为 ,
, 所以,当
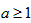 时,令
时,令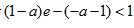 ,并解得
,并解得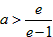 ,
,当
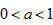 时,令
时,令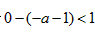 ,无解,
,无解,因此,a的取值范围是
 。
。
练习册系列答案
相关题目