题目内容
设函数A.0个 B.1个 C.2个 D.无数多个
答案:A
解析:
解析:
解:函数 , 一定是a<0, b>0, 否则会矛盾,∴ , 一定是a<0, b>0, 否则会矛盾,∴ 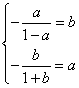 , 两式相加得 , 两式相加得
|

练习册系列答案
相关题目
 sin2x+m).
sin2x+m). 时,-4<f(x)<4恒成立,求实数m的取值范围.
时,-4<f(x)<4恒成立,求实数m的取值范围.