题目内容
(本题满分12分)设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx, sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间.
(2)当x∈ 时,-4<f(x)<4恒成立,求实数m的取值范围.
时,-4<f(x)<4恒成立,求实数m的取值范围.
【答案】
解:(1)f(x)=2cos2x+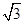 sin2x+m
sin2x+m
=2sin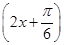 +m+1.
+m+1.
∴函数f(x)最小正周期T=π,
在[0,π]上的单调递增区间为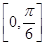 、
、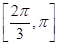 .……….(6分)
.……….(6分)
(2)∵当x∈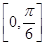 时,f(x)递增,
时,f(x)递增,
∴当x=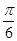 时,f(x)的最大值等于m+3.
时,f(x)的最大值等于m+3.
当x=0时,f(x)的最小值等于m+2.
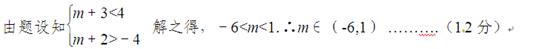
【解析】略

练习册系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;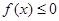 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求