题目内容
下列四个命题:①等轴双曲线的离心率为
| 2 |
②双曲线
| y2 |
| 49 |
| x2 |
| 25 |
| 5 |
| 7 |
③抛物线2y2=x的准线方程为x=-
| 1 |
| 8 |
④方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率.
其中真命题的序号是
分析:利用等轴双曲线中三参数的关系求出离心率,判断出①对;
双曲线的渐近线方程与双曲线方程的关系判断出②错;
利用抛物线的准线与抛物线方程的关系判断出③对;
求出二次方程的根,据椭圆、双曲线离心率的范围判断出④对.
双曲线的渐近线方程与双曲线方程的关系判断出②错;
利用抛物线的准线与抛物线方程的关系判断出③对;
求出二次方程的根,据椭圆、双曲线离心率的范围判断出④对.
解答:解:对于①,等轴双曲线中a=b,c=
a,离心率为
,①对
对于②
-
=-1的渐近线方程为
-
=0即y=±
x,②不对
对于③抛物线2y2=x即y2=
x,其准线方程为x=-
,③对
对于④,方程2x2-5x+2=0的两根为
或2,可分别作为椭圆和双曲线的离心率,④对
故答案为:①③④
| 2 |
| 2 |
对于②
| y2 |
| 49 |
| x2 |
| 25 |
| y2 |
| 49 |
| x2 |
| 25 |
| 7 |
| 5 |
对于③抛物线2y2=x即y2=
| 1 |
| 2 |
| 1 |
| 8 |
对于④,方程2x2-5x+2=0的两根为
| 1 |
| 2 |
故答案为:①③④
点评:解决圆锥曲线的方程有关的问题,一般利用三参数的关系,椭圆中有a2=b2+c2;双曲线中有c2=b2+a2一定要注意它们的区别.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ;
;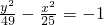 的渐近线方程为
的渐近线方程为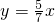 ;
;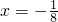 ;
;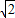 ;
;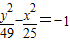 的渐近线方程为
的渐近线方程为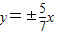 ;
;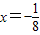 ;
;