题目内容
设a,b为正数,且a≠b,c=((1)比较c与1的大小;
(2)比较f(c)与f(![]() )的大小.
)的大小.
解:(1)若a>b>0,则![]() >1且a-b>0,
>1且a-b>0,
∴c=(![]() )a-b>(
)a-b>(![]() )0=1.
)0=1.
若b>a>0,则0<![]() <1且a-b<0,
<1且a-b<0,
∴c=(![]() )a-b>(
)a-b>(![]() )0=1.
)0=1.
综上,c>1.
(2)∵c>1,∴0<![]() <1.
<1.
∴c-1>0,![]() <0.
<0.
∴2c-1>1且![]() <1.
<1.
∴f(c)=|2c-1-1|=2c-1-1,
f(![]() )=|
)=|![]() -1|=1-
-1|=1-![]() .
.
∴f(c)-f(![]() )=2c-1-1+
)=2c-1-1+![]() -1=
-1=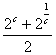 -2=
-2=
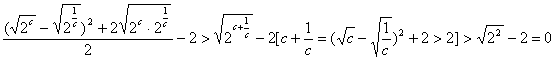
∴f(c)>f(![]() ).
).

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目