Question

设满足y≥|x-a|的点(x,y)的集合为A，满足y≤-|x|+b的点(x,y)的集合为B，其中a、b是正数，且A∩B≠.

(1)a、b之间有什么关系？

(2)求A∩B所表示的图形的面积.

Answer 1

解析：(1)不等式y≥|x-a|可化为或

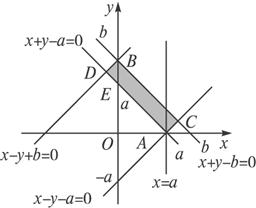
画出它所表示的平面区域如图所示.

不等式y≤-|x|+b可化为或将其表示的平面区域与集合A表示的平面区域画在同一坐标系中，如图所示，要使A∩B=，只要b≥a.

(2)由(1)知A∩B所表示的图形为矩形ACBD.

BE=b-a,在Rt△BDE中，∠DBE=45°，

∴BD=(b-a).

又AD=AE+DE=a+(b-a)=(b+a),

∴矩形面积S=BD·AD=(b²-a²).