题目内容
已知数列 中,
中,  ,
, (
( ).
).
(1)计算 ,
, ,
, ;
;
(2)猜想数列 的通项公式并用数学归纳法证明.
的通项公式并用数学归纳法证明.
【答案】
(1)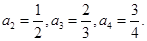 (2)
(2)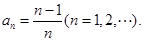 证明:当
证明:当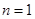 时,结论显然成立,假设当
时,结论显然成立,假设当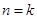 时,结论成立,即
时,结论成立,即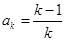 ,当
,当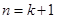 时,
时,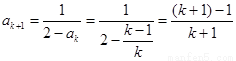 ,所以当
,所以当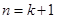 时,等式成立,由(1)(2)知,
时,等式成立,由(1)(2)知,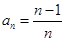 对一切自然数n都成立
对一切自然数n都成立
【解析】
试题分析:(1)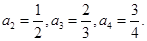 3分
3分
(2)猜想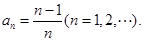 6分
6分
证明:(1)当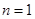 时,结论显然成立.
8分
时,结论显然成立.
8分
(2)假设当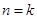 时,结论成立,即
时,结论成立,即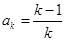
那么,当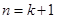 时,
时,
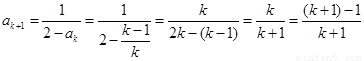
即当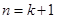 时,等式成立.
12分
时,等式成立.
12分
由(1)(2)知,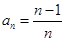 对一切自然数n都成立. 13分
对一切自然数n都成立. 13分
考点:归纳推理与数学归纳法
点评:数学归纳法用来证明与正整数有关的题目,其步骤:1,证明n取最小值时结论成立,2,假设 时命题成立,借此证明
时命题成立,借此证明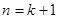 时命题成立,由1,2两步得证命题成立
时命题成立,由1,2两步得证命题成立

练习册系列答案
相关题目