题目内容
已知数列ξ中,满足a1=1且an+1=
,则
(n2an)=( )
| an |
| 1+nan |
| lim |
| n→∞ |
分析:先取倒数得:
-
=n,n分别取1,2,…n-1,再累加,可求通项,进而可求极限.
| 1 |
| an+1 |
| 1 |
| an |
解答:解:取倒数得:
-
=n
n分别取1,2,…n-1,累加得:
-
=1+2+…+n-1
∵a1=1
∴
=
∴an=
∴
(n2an)=
=2
故选C.
| 1 |
| an+1 |
| 1 |
| an |
n分别取1,2,…n-1,累加得:
| 1 |
| an |
| 1 |
| a1 |
∵a1=1
∴
| 1 |
| an |
| n2-n+2 |
| 2 |
∴an=
| 2 |
| n2-n+2 |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 2n2 |
| n2-n+2 |
故选C.
点评:本题以数列递推式为载体,考查数列的极限,关键是取倒数,求通项,进而求极限.

练习册系列答案
相关题目
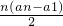 (n∈N*).
(n∈N*).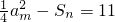 ,求m、n的值;
,求m、n的值;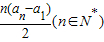
 am2-Sn=11,求m、n的值;
am2-Sn=11,求m、n的值;