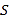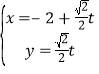题目内容
【题目】已知点
是抛物线
的顶点，
，
是
上的两个动点，且
.
（1）判断点
是否在直线
上？说明理由；
（2）设点
是△
的外接圆的圆心，求点的轨迹方程.
【答案】（1）点
在直线
上，理由见解析（2）
【解析】
（1）由抛物线的方程可得顶点
的坐标，设直线的方程，与抛物线联立求出两根之和及两根之积，求出数量积
，再由题意
可得直线恒过
，即得
在直线上；
（2）设
，
的坐标，可得直线
，
的斜率及线段，的中点坐标，进而求出线段，的中垂线的方程，两个方程联立求出外接圆的圆心
的坐标，由（1）可得的横纵坐标关于参数
的表达式，消参数可得的轨迹方程．
(1) 点在直线上.理由如下，
由题意, 抛物线
的顶点为
因为直线与抛物线有2个交点，
所以设直线AB的方程为
联立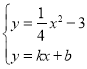
得到
，
其中
，
所以
，
因为
所以
，
所以
，
解得
，
经检验，满足
，
所以直线AB的方程为
，恒过定点.
（2）因为点是
的外接圆的圆心，所以点是三角形
三条边的中垂线的交点，
设线段的中点为
，线段的中点为为
，
因为，设
，
，
，
所以
，
，
，
，
，
，
所以线段的中垂线的方程为：
，
因为在抛物线上，所以
，
的中垂线的方程为：
，即
，
同理可得线段的中垂线的方程为：
，
联立两个方程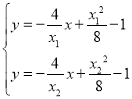
，解得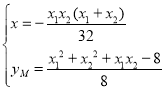
，
由（1）可得
，
，
所以
，
，
即点
，所以
，
即点的轨迹方程为：．
练习册系列答案
阅读快车系列答案
相关题目
