题目内容
14、设A（0，0），B（4，0），C（t+4，3），D（t，3）（t∈R）．记N（t）为平行四边形ABCD内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则N（0）=
6
，N（t）的所有可能取值为6、7、8
．分析：作出平行四边形，结合图象得到平行四边形中的整数点的个数．
解答：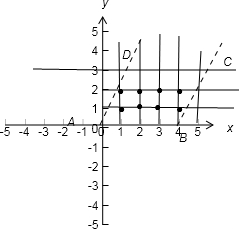
解：当t=0时，平行四边形ABCD内部的整点有（1，1）；（1，2）；（2，1）；（2，2）；（3，1）；（3，2）共6个点，
所以N（0）=6
作出平行四边形ABCD
将边OD，BC变动起来，结合图象得到N（t）的所有可能取值为6，7，8
故答案为6；6，7，8
解：当t=0时，平行四边形ABCD内部的整点有（1，1）；（1，2）；（2，1）；（2，2）；（3，1）；（3，2）共6个点，所以N（0）=6
作出平行四边形ABCD
将边OD，BC变动起来，结合图象得到N（t）的所有可能取值为6，7，8
故答案为6；6，7，8
点评：本题考查画可行域、考查数形结合的数学思想方法．
练习册系列答案
相关题目
设A在x轴上，它到点P(0，
，3)的距离等于到点Q（0，1，-1）的距离的两倍，那么A点的坐标是（ ）
| 2 |
| A、（1，0，0）和（-1，0，0） | ||||||||
| B、（2，0，0）和（-2，0，0） | ||||||||
C、（
| ||||||||
D、（-
|